All AP Calculus AB Resources
Example Questions
Example Question #35 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Evaluate the following integral
To evaluate the integral, we use the fact that the antiderivative of 





Example Question #36 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Calculate the following integral.
Calculate the following integral.
To do this problem, we need to recall that integrals are also called antiderivatives. This means that we can calculate integrals by reversing our integration rules.
Thus, we can have the following rules.
Using these rules, we can find our answer:

Will become:
And so our answer is:
Example Question #111 : Integrals
Integrate:
The integral of the function is equal to
and was found using the following rule:
Finally, we evaluate by plugging in the upper bound into the resulting function and subtracting the resulting function with the lower bound plugged in:
Example Question #112 : Integrals
Solve:
The integral is equal to
The rules used to integrate are

Now, we solve by plugging in the upper bound of integration and then subtracting the result of plugging in the lower bound of integration:
Example Question #41 : Techniques Of Antidifferentiation
Integrate:
The integral is equal to
and was found using the following rule:
Example Question #41 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Integrate:
The integral is equal to
The following rule was used to integrate:
Now, we find the numerical answer by plugging in the upper bound of integration and subtracting what we get from plugging in the lower bound of integration:
Example Question #41 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Integrate:
Undefined
The integral is equal to
and was found using the identical rule.
Evaluating by plugging in the upper bound and subtracting from what we get from plugging in the lower bound, we get
Example Question #1 : Antiderivatives By Substitution Of Variables
Use a change of variable (aka a u-substitution) to evaluate the integral,
Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example, 


Now differentiate with respect to 


Looking at equation (2), we can solve for 


Now proceed with the integration with respect to 

Now write the result in terms of 
Example Question #1 : Antiderivatives By Substitution Of Variables
Use u-subtitution to fine
Let
Then
Now we can subtitute
Now we substitute back
Example Question #3 : Antiderivatives By Substitution Of Variables
Evaluate
We can use substitution for this integral.
Let 
then 
Multiplying this last equation by 

Now we can make our substitutions














All AP Calculus AB Resources


















![\int_{0}^{1}[x^2+\frac{x}{2}]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1029744/gif.latex)





![\int_{0}^{1}[x^2+\frac{x}{2}]dx= \frac{x^3}{3}+\frac{x^2}{4}\left.\begin{matrix} 1\\ 0 \end{matrix}\right|](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1029745/gif.latex)



































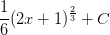
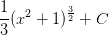


![= \frac{1}{2}\left[\frac{1}{\frac{1}{2}+1}u^{\frac{1}{2}+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)























