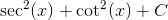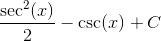All AP Calculus AB Resources
Example Questions
Example Question #71 : Techniques Of Antidifferentiation
Solve:
To integrate, we must make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used for integration:
Replacing u with our original x term, we get
Example Question #71 : Techniques Of Antidifferentiation
Calculate:
Rewrite the integrand as follows:

The integral can be rewritten as
Now, use 

The limits of integration can be rewritten as
The integral becomes
Integrate:

the correct response.
Example Question #73 : Techniques Of Antidifferentiation
Evaluate the following integral
The integral can be solved by using a variable substitution

Replacing 

Example Question #961 : Ap Calculus Ab
Evaluate the following integral
We solve the problem by making a variable substitution

The integral then becomes
Substituting 

Example Question #75 : Techniques Of Antidifferentiation
Solve:
To integrate, it is easiest to break the integral into the sum of two integrals:
To integrate the first integral, we must make the following substitution:
The derivative was found using the rule itself.
Rewriting the first integral in terms of u and integrating, we get
which was found using the rule itself.
Replacing u with our original x term, we get
The second integral is equal to
and was found using the following rule:
Adding our two results, and combining the two constants of integration into a single integration constant, we get
Example Question #76 : Techniques Of Antidifferentiation
Calculate the integral in the following expression:
The simplest path to follow when trying to integrate a lot of trig expressions is often to put everything in terms of sin(x) and cos(x). Doing this for the above expressions yields:
Next, we look for expressions that we know how to integrate, based on the following facts:
And, of course, the simpler derivatives of sin(x) and cos(x).
Looking for these above expressions in our integral, we note that
Breaking this up into two integrals, we see that the second immediately can be simplified into -csc(x) + C. The first, while a bit more tricky, just requires you to realize that sec(x)tan(x) is the derivative of sec(x). Thus, if you use a substitution of variables (u-sub) with u = sec(x), you will get,
and
In this form, it is clear to see that the integral is just 
Combining our two integrals, we get a final answer of
Example Question #77 : Techniques Of Antidifferentiation
Evaluate the integral
To evaluate the integral, we make a variable substitution for

The integral then becomes
Substituting 

Example Question #78 : Techniques Of Antidifferentiation
Many integrals are unsolvable, the techniques you learn are for special cases of integrals, and are used in the scenarios where the integral is possible to do by hand.
Evaluate the integral by using integration by substitution.

So, unlike with derivatives, there is no equivalent for the chain rule of the product rule for integrals. Anytime you see a function within a function (a compound function) and/or the product of more than one function inside an integral, you can't just take the integral. In this case, we are able to perform a substitution. So the goal with a substitution is to replace all of the x variables (including dx) with another variable (we use u, and du).
So we can set
which gives us
So this changes our integral to:
Which just turns out to:

After replacing u for what is originally was, we end up with:
Example Question #79 : Techniques Of Antidifferentiation
Many integrals are unsolvable, the techniques you learn are for special cases of integrals, and are used in the scenarios where the integral is possible to do by hand.
Evaluate this integral using substitution.
So, unlike with derivatives, there is no equivalent for the chain rule of the product rule for integrals. Anytime you see a function within a function (a compound function) and/or the product of more than one function inside an integral, you can't just take the integral. In this case, we are able to perform a substitution. So the goal with a substitution is to replace all of the x variables (including dx) with another variable (we use u, and du).
For this problem, we set
This gives us
So the thing to note with substitutions is that the 

So making these substitutions gives:
solving this integral gives:
Substituting the u back into the equation gives us a final answer of:
Example Question #31 : Antiderivatives By Substitution Of Variables
We are going to use U-substitution
Looking at the original
Let
Then
And now we can use our anti derivative rules (don't forget your constant!)
Finally, substitute back in for u
Certified Tutor
Certified Tutor
All AP Calculus AB Resources