Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Derivative rules for sums, products, and quotients of functions

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function,

$y =x^2\sin(3x)$

Possible Answers:

$\frac{dy}{dx} =3x^2\cos(3x)+2x\sin(3x)$

$\frac{dy}{dx} =x[3x\cos(3x)+2]$

$\frac{dy}{dx} =-3x^2\cos(x)+2x\sin(x)$

$\frac{dy}{dx} =6x\cos(3x)$

$\frac{dy}{dx} =x^2\cos(3x)+2x\cos(3x)$

Correct answer:

$\frac{dy}{dx} =3x^2\cos(3x)+2x\sin(3x)$

Explanation:

$y =x^2\sin(3x)$

Differentiate both sides and proceed with the product rule:

$\frac{dy}{dx}=\frac{d}{dx}[x^2\sin(3x)]$ (1)

$\frac{dy}{dx}= x^2\frac{d}{dx}\sin(3x)+ \sin(3x)\frac{d}{dx}x^2$

Evaluate the derivatives in each term. For the first term,

$=x^2\underbrace{\frac{d}{dx}\sin(3x)} + \sin(3x)\frac{d}{dx}x^2$ (2)

apply the chain rule,

$\frac{d}{dx}sin(3x)=3\cos(3x)$

So now the first term in equation (2) can be written,

$x^2\frac{d}{dx}\sin(3x)=x^2[3\cos(3x)]=3x^2\cos(3x)$ (3)

The second term in equation (2) is easy, this is just the product of $\sin(3x)$ multiplied by the derivative of x^2 ,

$\sin(3x)\frac{d}{dx}x^2 = 2x\sin(3x)$ (4)

Combine equations (3) and (4) to write the derivative,

$\frac{dy}{dx} =3x^2\cos(3x)+2x\sin(3x)$

Report an Error

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative.

$\sin (x)x^2$

Possible Answers:

$\cos (x)x^2+2x\sin (x)$

$\sin (x)x^2+2x\sin (x)$

$\cos (x)x^2+2x^2\sin (x)$

$\cos (x)x+2x\sin (x)$

Correct answer:

$\cos (x)x^2+2x\sin (x)$

Explanation:

Use the product rule to find the derivative.

$\cos (x)x^2+2x\sin (x)$

Report an Error

Example Question #3 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative.

x^3+4x^2-x

Possible Answers:

x^2+4x

3x^2+8x-1

4x^4

x^2+4x-1

Correct answer:

3x^2+8x-1

Explanation:

Use the power rule to find the derivative.

$\frac{d}{dx}x^3=3x^2$

$\frac{d}{dx}4x^2=8x$

$\frac{d}{dx}-x=-1$

Thus, the derivative is 3x^2+8x-1

Report an Error

Example Question #4 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) given $f(x)=3sin(x^2)*e^{2x-1}$

Possible Answers:

$f'(x)=6xcos(x^2)*e^{2x-1}+3sin(x^2)*(2x-1)e^{2x-2}$

$f'(x)=6e^{2x-1}(xcos(x^2)+sin(x^2))$

$f'(x)=\frac{6e^{2x-1}(xcos(x^2)*sin(x^2))}{e^{4x-2}}$

$f'(x)=6e^{2x-1}(cos(2x)+sin(x^2))$

$f'(x)=12xe^{2x-1}(cos(x^2))$

Correct answer:

$f'(x)=6e^{2x-1}(xcos(x^2)+sin(x^2))$

Explanation:

Here we use the product rule: $\frac{\mathrm{d} }{\mathrm{d} x}(F(x)\cdot G(x))=F'(x)\cdot G(x)+F(x)\cdot G'(x)$

Let F(x)=3sin(x^2) and $G(x)=e^{2x-1}$

Then $F'(x)=3cos(x^2)\cdot2x$ (using the chain rule)

and $G'(x)=e^{2x-1}\cdot2$ (using the chain rule)

Subbing these values back into our equation gives us

$f'(x)=3cos(x^2)\cdot2x\cdot e^{2x-1}+3sin(x^2)\cdot e^{2x-1}\cdot2$

Simplify by combining like-terms

$f'(x)=6xcos(x^2)\cdot e^{2x-1}+6sin(x^2)\cdot e^{2x-1}$

and pulling out a $6e^{2x-1}$ from each term gives our final answer

$f'(x)=6e^{2x-1}(xcos(x^2)+sin(x^2))$

Report an Error

Example Question #5 : Derivative Rules For Sums, Products, And Quotients Of Functions

If $f(x)=\pi\sin(ex)$ , evaluate f'(0) .

Possible Answers:

$\pi$

$e\pi$

Correct answer:

$e\pi$

Explanation:

When evaluating the derivative, pay attention to the fact that $e,\pi$ are constants, (not variables) and are treated as such.

$f'(x)=\pi\cos(ex)\times (ex)'=e\pi\cos(ex)$ .

and hence

$f'(0)=e\pi\cos(e(0))=e\pi$ .

Report an Error

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

If f(x)=1+x+x^2+x^3+x^4 , evaluate f'(2)

Possible Answers:

Correct answer:

Explanation:

To obtain an expression for f'(x) , we can take the derivative of f(x) using the sum rule.

f'(x)=0+1+2x+3x^2+4x^3 .

Substituting into this equation gives us

f'(2) =0+1+4+12+32

=49 .

Report an Error

Example Question #2 : Derivative Rules For Sums, Products, And Quotients Of Functions

If $f(x)=\frac{x\tan^{-1}(x)}{\ln(x)}$ , find f'(x) .

Possible Answers:

$\frac{\ln(x)(\frac{x}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{(\ln(x))^2}$

$\frac{\ln(x)(\frac{1}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{(\ln(x))^2}$

$\frac{\ln(x)(\frac{x+1}{1+x^2})-\tan^{-1}x}{\ln(x^2)}$

$\frac{\ln(x)(\frac{1}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{\ln(x^2)}$

$\frac{\frac{1}{x}(\frac{x}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{\ln(x^2)}$

Correct answer:

$\frac{\ln(x)(\frac{x}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{(\ln(x))^2}$

Explanation:

To find f'(x) , we will need to use the quotient rule; $\frac{gf'-fg'}{g^2}$ .

$f(x)= \frac{x\tan^{-1}x}{\ln(x)}$ . Start

$f'(x)= \frac{(\ln(x))(x\tan^{-1}x)'-(x\tan^{-1}x)(\ln(x))'}{(\ln(x))^2}$ . Use the quotient rule.

$= \frac{(\ln(x))(x(\frac{1}{1+x^2})+1(\tan^{-1}x))-(x\tan^{-1}x)(\frac{1}{x})}{(\ln(x))^2}$ . Take the derivatives inside of the quotient rule. The derivative of $x\tan^{-1}x$ uses the product rule.

$=\frac{\ln(x)(\frac{x}{1+x^2}+\tan^{-1}x)-\tan^{-1}x}{(\ln(x))^2}$ . Simplify to match the correct answer.

Report an Error

Example Question #8 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following equation:

$h(x) = \sin(x)\cos(x)$

Possible Answers:

$\cos ^{2}(x)$

$-\sin(x)\cos(x)$

$\cos^{2}(x)-\sin^{2}(x)$

$\cos ^{2}(x)+\sin^{2}(x)$

None of the other answers

Correct answer:

$\cos^{2}(x)-\sin^{2}(x)$

Explanation:

Because this problem contains two functions multiplied together that can't be simplified any further, it calls for the product rule, which states that $\frac{d}{dx}(f(x)g(x)) = f{}'(x)g(x) + f(x)g{}'(x)$ .

By using this rule, we get the answer:

$\cos(x)\cos(x) + \sin(x)(-\sin (x))$

By simplifying, we conclude that the derivative is equal to

$\cos ^{2}(x)-\sin ^{2}(x)$ .

Report an Error

Example Question #9 : Derivative Rules For Sums, Products, And Quotients Of Functions

$\begin{align*}&\text{Calculate the derivative of the function}\\&-\frac{(114cos(19x))}{x^{20}}\end{align*}$

Possible Answers:

$\frac{120}{x^{21}}- 361sin(19x)$

$\frac{(2280cos(19x))}{x^{21}}+\frac{ (2166sin(19x))}{x^{20}}$

$-\frac{(43320sin(19x))}{x^{21}}$

$-\frac{ (43320cos(19x))}{x^{21}}-\frac{ (43320sin(19x))}{x^{20}}$

Correct answer:

$\frac{(2280cos(19x))}{x^{21}}+\frac{ (2166sin(19x))}{x^{20}}$

Explanation:

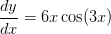
$\begin{align*}&\text{The function that we have been given can be seen as two smaller functions}\\&\text{multiplied together, the first being: }cos(19x)\\&\text{and the second being: }\frac{1}{x^{20}}\\&\text{With the product scaled by }-114\\&\text{To perform the derivative, }\text{ we'll wish to use the product rule, }d[uv]=udv+vdu\\&\text{along with the following:}\\&d[cos(ax)]=-asin(ax)dx\\&d[x^a]=ax^{a-1}dx\\&\text{From the above we can continue:}\\&u=cos(19x);du=-19sin(19x)\\&v=\frac{1}{x^{20}};dv=-\frac{20}{x^{21}}\\&\text{We can then combine these terms (Don't forget the scalar!)}\\&\text{So the derivative is:}\\&\frac{(2280cos(19x))}{x^{21}}+\frac{ (2166sin(19x))}{x^{20}}\end{align*}$

Report an Error

Example Question #10 : Derivative Rules For Sums, Products, And Quotients Of Functions

$\begin{align*}&\text{Take the derivative with respect to }x\text{ of the function}\\&y=-\frac{(380tan(17x))}{2^{(20x)}}\end{align*}$

Possible Answers:

$\frac{(7600\cdot (17tan(17x)^{2} + 17))}{2^{(20x)}}+\frac{ (129200tan(17x)ln(2))}{2^{(20x)}}$

$\frac{(20ln(2)\cdot (6460tan(17x)^{2} + 6460))}{2^{(20x)}}$

$\frac{(7600tan(17x)ln(2))}{2^{(20x)}}-\frac{ (380\cdot (17tan(17x)^{2} + 17))}{2^{(20x)}}$

$\frac{(380ln(2))}{2^{(20x)}}+ 340tan(17x)^{2} + 340$

Correct answer:

$\frac{(7600tan(17x)ln(2))}{2^{(20x)}}-\frac{ (380\cdot (17tan(17x)^{2} + 17))}{2^{(20x)}}$

Explanation:

$\begin{align*}&\text{The function that we have been given can be seen as two smaller functions}\\&\text{multiplied together, the first being: }tan(17x)\\&\text{and the second being: }\frac{1}{2^{(20x)}}\\&\text{With the product scaled by }-380\\&\text{To perform the derivative, }\text{ we'll wish to use the product rule, }d[uv]=udv+vdu\\&\text{along with the following:}\\&d[tan(ax)]=\frac{adx}{cos^2(ax)}=(atan^2(ax)+a)dx\\&d[b^{ax}]=ab^{ax}ln(b)sx\\&\text{From the above we can continue:}\\&u=tan(17x);du=17tan(17x)^{2} + 17\\&v=\frac{1}{2^{(20x)}};dv=-\frac{(20ln(2))}{2^{(20x)}}\\&\text{We can then combine these terms (Don't forget the scalar!)}\\&\text{So the derivative is:}\\&\frac{(7600tan(17x)ln(2))}{2^{(20x)}}-\frac{ (380\cdot (17tan(17x)^{2} + 17))}{2^{(20x)}}\end{align*}$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

View AP Calculus AB Tutors

Bruce
Certified Tutor

University of Florida, Bachelor of Science, Mathematics. University of Florida, Master of Science, Mathematics.

View AP Calculus AB Tutors

Rahul
Certified Tutor

University of Calgary , Master's/Graduate, Aerospace engineering .

View AP Calculus AB Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Boston, GRE Tutors in Miami, SSAT Tutors in New York City, ACT Tutors in Dallas Fort Worth, Calculus Tutors in San Diego, English Tutors in Dallas Fort Worth, ISEE Tutors in New York City, Reading Tutors in Philadelphia, Calculus Tutors in Dallas Fort Worth, Calculus Tutors in Chicago

Popular Courses & Classes

ISEE Courses & Classes in Houston, GRE Courses & Classes in Chicago, SSAT Courses & Classes in San Diego, ACT Courses & Classes in Los Angeles, ACT Courses & Classes in Seattle, LSAT Courses & Classes in Seattle, ISEE Courses & Classes in Miami, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta, SAT Courses & Classes in Los Angeles

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Phoenix, MCAT Test Prep in Miami, ACT Test Prep in Los Angeles, SAT Test Prep in San Diego, ISEE Test Prep in New York City, ISEE Test Prep in Denver, GRE Test Prep in San Diego, MCAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Derivative rules for sums, products, and quotients of functions

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #3 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #4 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #5 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #2 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #8 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #9 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #10 : Derivative Rules For Sums, Products, And Quotients Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: