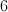We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #104 : Chain Rule And Implicit Differentiation

Find the derivative of $\tan^2(\sin x)$ .

Possible Answers:

$2\tan(\sin x)\sec^2(\sin x)$

$\tan(\sin x)\sec(\sin x)$

$2\tan(\sin x)\sec^2(\sin x)\cos x$

$2\tan(\sin x)\sec x$

$\sec^4(\sin x)\cos x$

Correct answer:

$2\tan(\sin x)\sec^2(\sin x)\cos x$

Explanation:

This problem requires us to use the chain rule twice.

First, take the derivative of $(\tan x)^2$ .

$(\tan^2 x)'=2\tan x sec^2 x$

Now substitute $\sin x$ for and multiply by the derivative of $\sin x$ .

$2\tan(\sin x)\sec^2(\sin x)\cos x$ is our final answer.

Report an Error

Example Question #103 : Chain Rule And Implicit Differentiation

Given yx^2 + 2y + x = 10 , calculate the slope of the tangent line when x = 1 .

Possible Answers:

$-\frac{7}{3}$

$-\frac{17}{9}$

Correct answer:

$-\frac{7}{3}$

Explanation:

The slope of the tangent line is found by taking the derivative. In this case, because we don't have the function defined explicitly, we'll have to use implicit differentiation to get

$2xy + x^2\frac{\mathrm{d} y}{\mathrm{d} x} + 2\frac{\mathrm{d} y}{\mathrm{d} x} + 1 = 0$

Where the first two terms come from product rule. Factoring out a dy/dx and moving the other terms to the right, we get

$\frac{\mathrm{d} y}{\mathrm{d} x}(x^2 + 2) = -2xy - 1$

And solving for dy/dx, we get

$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{-2xy - 1}{x^2 + 2}$ .

As the problem doesn't give us a y value, we'll need to go back to the original equation to find it. Plugging in x = 1, we have

y(1)^2 + 2y + 1 = 10

And simplifying yields

3y = 9 ; y = 3

Plugging the point (1, 3) into our expression for dy/dx, we have

$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{-2(1)(3) - 1}{1^2 + 2} = -\frac{7}{3}$

Alternatively, this expression could have been solved for explicitly by factoring a y term out. Note,

yx^2 + 2y + x = y(x^2 + 2) + x = 10

And thus, $y = \frac{10-x}{x^2 + 2}$ . Using quotient rule, we know the derivative of this

is $\frac{-x^2 - 2 - 2x(10-x)}{(x^2 + 2)^2}$ .

Evaluated at x=1, this becomes

$\frac{-(1)^2 - 2 - 2(10-1)}{((1)^2 + 2)^2} = -\frac{21}{9} = -\frac{7}{3}$

Report an Error

Example Question #104 : Chain Rule And Implicit Differentiation

For the equation, $x \sin(y) + y\cos(y) = 0$ , find $\frac{\mathrm{d} y}{\mathrm{d} x}$ .

Possible Answers:

$\frac{\mathrm{d} y}{\mathrm{d} x}=\cot(y)$

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{-\sin(y)}{x\cos(y)-y\sin(y)+\cos(y)}$

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1}{x\cos(y)+\cos(y)+y}$

$\frac{\mathrm{d} y}{\mathrm{d} x}= y\tan(y)-\tan(y) -x$

Correct answer:

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{-\sin(y)}{x\cos(y)-y\sin(y)+\cos(y)}$

Explanation:

Finding $\frac{\mathrm{d} y}{\mathrm{d} x}$ for an equation of this complexity requires implicit differentiation.

We need to take the derivative of both sides with respect to x.

For $x\sin(y)$ , we will apply the product rule and chain rule.

The product rule is as follows: $\frac{\mathrm{d} }{\mathrm{d} x}(f\cdot g)= {\color{Red} f}\cdot{\color{Green} g'} + {\color{Green} g}\cdot{\color{Red} f'}$ , where f and g are the two factors of the expression. In this case, and will be and $\sin(y)$ respectively. When we find ${\color{Green} g'}$ , we will use the chain rule. This is because the inside of the $\sin$ contains variables other than x. Recall that the derivative of with respect to is $\frac{\mathrm{d} y}{\mathrm{d} x}$ .

This all means that ${\color{Green} g'}=\cos(y)\cdot(\frac{\mathrm{d} y}{\mathrm{d} x})$

Observe that ${\color{Red} f'}=\frac{\mathrm{d} }{\mathrm{d} x}(x)$ which is just 1.

Applying all this we find that the derivative of $x\sin(y)$ is

${\color{Red} x}\cdot{\color{Green} \cos(y)\cdot(\frac{\mathrm{d} y}{\mathrm{d} x})} + {\color{Green} \sin(y)}\cdot{\color{Red} (1)}$ .

Now we will find the derivative of the next term, $y \cos(y)$ . This will also require product rule and chain rule. For this product rule, ${\color{Red} f}$ and ${\color{Green} g}$ will be ${\color{Red} y}$ and ${\color{Green} \cos(y)}$ respectively.

${\color{Red} f'}$ will be the derivative of with respect to , which is ${\color{Red} \frac{\mathrm{d} y}{\mathrm{d} x}}$ .

${\color{Green} g'}$ will require the chain rule. The derivative of $\cos$ is $-\sin$ , and the derivative of with respect to is $\frac{\mathrm{d} y}{\mathrm{d} x}$ .

This means that ${\color{Green} g' }= {\color{Green} -\sin(y)(\frac{\mathrm{d} y}{\mathrm{d} x})}$ .

Assembling the power rule gives the derivative of the second term as

${\color{Red} y}\cdot{\color{Green} (-\sin(y))(\frac{\mathrm{d} y}{\mathrm{d} x})} +{\color{Green} \cos(y)}\cdot{\color{Red} \frac{\mathrm{d} y}{\mathrm{d} x}}$

For the right hand side of the equation, the derivative of is still .

Putting all three derivatives together into one equation yields the following:

$x\cos(y)(\frac{\mathrm{d} y}{\mathrm{d} x}) + \sin(y) -y\sin(y)(\frac{\mathrm{d} }{\mathrm{d} x}) + \cos(y)(\frac{\mathrm{d} y}{\mathrm{d} x})=0$

The next step in implicit differentiation is solving for $\frac{\mathrm{d} y}{\mathrm{d} x}$ . To do this we move all terms that have no $\frac{\mathrm{d} y}{\mathrm{d} x}$ factor to one side, and all terms with a $\frac{\mathrm{d} y}{\mathrm{d} x}$ factor to the other side.

In this case, we already have all $\frac{\mathrm{d} y}{\mathrm{d} x}$ terms on the left, so we will move the non- $\frac{\mathrm{d} y}{\mathrm{d} x}$ terms to the right side.

$x\cos(y)(\frac{\mathrm{d} y}{\mathrm{d} x}) -y\sin(y)(\frac{\mathrm{d} }{\mathrm{d} x}) + \cos(y)(\frac{\mathrm{d} y}{\mathrm{d} x})=-\sin(y)$

Now we can pull the common factor of $\frac{\mathrm{d} y}{\mathrm{d} x}$ out of the left side. We will then divide by what is remaining.

$\frac{\mathrm{d} y}{\mathrm{d} x}[x\cos(y)-y\sin(y)+\cos(y)]=-\sin(y)$

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{-\sin(y)}{x\cos(y)-y\sin(y)+\cos(y)}$

This is the final answer. It cannot be simplified.

Report an Error

Example Question #201 : Computation Of The Derivative

Let $f(x)=[e^{2x}+\sin(e^{x^3})]^3$ . Find the derivative, f'(x) .

Possible Answers:

$f'(x)=6e^{6x}+9x^2e^{x^3}\sin^2(e^{x^3})\cos(e^{x^3})$

$f'(x)=[2e^{2x}+3x^2e^{x^3}\cos(e^{x^3})]^3$

$f'(x)=3[e^{2x}+\sin(e^{x^3})]^2[e^{2x}+\cos(e^{x^3})]$

$f'(x)=3[e^{2x}+\sin(e^{x^3})]^2[2e^{2x}+3x^2e^{x^3}\cos(e^{x^3})]$

Correct answer:

$f'(x)=3[e^{2x}+\sin(e^{x^3})]^2[2e^{2x}+3x^2e^{x^3}\cos(e^{x^3})]$

Explanation:

The shortest and simplest way to find the derivative of this function is to use the Chain Rule. The Chain Rule definition is $[f(g(x))]' = f'(g(x))\cdot g'(x)$ . This is somewhat difficult to read and work with at first. Putting it in words helps though. What this definition states is that the derivative of "layered functions" is the derivative of the outer function times the derivative of the inner function. When I say "layered functions", I mean functions inside other functions. In this problem, we have the function, $(e^{2x}+\sin(e^{x^3}))$ , inside of a cubic function , (u)^3 , where is holding the place of the inner function. The outer function is the cubic, while the inner function is the $(e^{2x}+\sin(e^{x^3}))$ .

Applying the chain rule to this pair of layers means applying the power rule to the outer function, then multiplying it by the derivative of the inner function. Doing so gives

$3(inner function)^2\cdot(inner function)'$

We will need to find the derivative of the inner function, $(e^{2x}+\sin(e^{x^3}))$ , but first we will write the expression using the actual inner function.

$3(e^{2x}+\sin(e^{x^3}))^2\cdot(e^{2x}+\sin(e^{x^3}))'$ .

To find $(e^{2x}+\sin(e^{x^3}))'$ , we will take the derivative of the two terms inside separately.

The derivative of $e^{2x}$ is $e^{2x}\cdot(2)$ .

The derivative of $\sin(e^{x^3})$ is another Chain Rule. We take the derivative of outer function, $\sin$ , to get $\cos$ of the same inner function. Then we multiply it by the derivative of the inner function. The derivative of $e^{x^3}$ is $e^{x^3}\cdot(3x^2)$ .

Putting these together we get the following for the derivative of $(e^{2x}+\sin(e^{x^3}))$ :

$e^{2x}(2)+ \cos(e^{x^3})(e^{x^3}(3x^2))$

Simplifying it, we get

$2e^{2x} + 3x^2e^{x^3}\cos(e^{x^3})$

Putting this at the end of the original chain rule we have

$f'(x)=3(e^{2x}+\sin(e^{x^3}))^2\cdot(2e^{2x}+ 3x^2e^{x^3}\cos(e^{x^3}))$

This cannot be simplified, so it is the final answer

Report an Error

Example Question #101 : Chain Rule And Implicit Differentiation

Find f'(x) if $f(x)=sin(e^{x})$

Possible Answers:

e^xx(cos(x))

-e(cos(e^x))

e^x(cos(e^x))

$\frac{cos(e^x)}{ln(x)}$

-ln(cos(x))

Correct answer:

e^x(cos(e^x))

Explanation:

$\frac{d}{du}[sin(u)]=cos(u)$

$\frac{d}{du}[e^u]=e^u \cdot u'$

According to the chain rule $\frac{d}{du}[f(g(u))]=f'(g(u)) \cdot g'(u)$ .

Therefore, the derivative we are looking for will be

$cos(e^x) \cdot e^x \cdot 1 = e^x(cos(e^x))$

Report an Error

Example Question #102 : Chain Rule And Implicit Differentiation

Use implicit differentiation to calculate $\frac{\mathrm{d}y }{\mathrm{d} x}$ for the following equation: $e^{x}-cos(y)=x$

Possible Answers:

$(1+e^{x})(sec(y)$

$(1+e^{x})(csc(y)$

$(1-e^{x})(sec(y)$

$(1-e^{x})(csc(y))$

Correct answer:

$(1-e^{x})(csc(y))$

Explanation:

$e^{x}-cos(y)=x$

Differentiate both sides of the equation: $\frac{\mathrm{d} }{\mathrm{d} x}(e^{x}-cos(y)=x)$

Simplify: $e^{x}-\frac{\mathrm{d} }{\mathrm{d} x}cos(y)=1$

Use implicit differentiation to evaluate $\frac{\mathrm{d} }{\mathrm{d} x}cos(y)$ : $e^{x}-(-siny)\frac{\mathrm{d} y}{\mathrm{d} x}=1$

Simplify: $e^{x}+siny\frac{\mathrm{d} y}{\mathrm{d} x}=1$

Subtract $e^{x}$ from both sides of the equation: $siny\frac{\mathrm{d} y}{\mathrm{d} x}=1-e^{x}$

Divide both sides of the equation by siny: $\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1-e^{x}}{sin(y)}$

Simplify: $\frac{\mathrm{d} y}{\mathrm{d} x}=1-e^{x}(csc(y))$

Solution: $\frac{\mathrm{d} y}{\mathrm{d} x}=1-e^{x}(csc(y))$

Report an Error

Example Question #1 : Interpretations And Properties Of Definite Integrals

If f(1) = 12, f' is continuous, and the integral from 1 to 4 of f'(x)dx = 16, what is the value of f(4)?

Possible Answers:

Correct answer:

Explanation:

You are provided f(1) and are told to find the value of f(4). By the FTC, the following follows:

(integral from 1 to 4 of f'(x)dx) + f(1) = f(4)

16 + 12 = 28

Report an Error

Example Question #1 : Interpretations And Properties Of Definite Integrals

Find the limit.

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

Possible Answers:

–6

nonexistent

Correct answer:

Explanation:

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

Use L'Hopitals rule to find the limit.

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

lim as n approaches infiniti of ((12n²) – 6)/((3n²) – 4n + 6)

lim as n approaches infiniti of 24n/(6n – 4)

lim as n approaches infiniti of 24/6

The limit approaches 4.

Report an Error

Example Question #1 : Interpretations And Properties Of Definite Integrals

If a particle's movement is represented by $p=3t^{2}-t+16$ , then when is the velocity equal to zero?

Possible Answers:

$\frac{1}{6}$

Correct answer:

$\frac{1}{6}$

Explanation:

The answer is $\frac{1}{6}$ seconds.

$p=3t^{2}-t+16$

$v=p'=6t-1$

now set v=0 because that is what the question is asking for.

$v=0=6t-1$

$t=\frac{1}{6}$ seconds

Report an Error

Example Question #3 : Interpretations And Properties Of Definite Integrals

A particle's movement is represented by $p=-t^{2}+12t+2$

At what time is the velocity at it's greatest?

Possible Answers:

Correct answer:

Explanation:

The answer is at 6 seconds.

$p=-t^{2}+12t+2$

We can see that this equation will look like a upside down parabola so we know there will be only one maximum.

$v=p'=-2t+12$

Now we set v=0 to find the local maximum.

$v=0=-2t+12$

$t=6$ seconds

Report an Error

View AP Calculus AB Tutors

Steven
Certified Tutor

University of Louisville, Bachelor of Science, Mechanical Engineering. University of Phoenix-Louisville Campus, Master of Eng...

View AP Calculus AB Tutors

MrG
Certified Tutor

Long Island University-Brooklyn Campus, Master of Science, Applied Mathematics.

View AP Calculus AB Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Denver, Spanish Tutors in Miami, English Tutors in Los Angeles, ISEE Tutors in Washington DC, SSAT Tutors in San Diego, Algebra Tutors in Seattle, French Tutors in Houston, English Tutors in Atlanta, ACT Tutors in Houston, Statistics Tutors in Dallas Fort Worth

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, Spanish Courses & Classes in Atlanta, GMAT Courses & Classes in Chicago, GRE Courses & Classes in Chicago, LSAT Courses & Classes in Boston, SAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Houston, LSAT Courses & Classes in Denver, MCAT Courses & Classes in Denver, LSAT Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in Houston, GRE Test Prep in Chicago, SSAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in Chicago, SAT Test Prep in San Diego, MCAT Test Prep in Houston, GRE Test Prep in Atlanta, GRE Test Prep in Philadelphia, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #104 : Chain Rule And Implicit Differentiation

Example Question #103 : Chain Rule And Implicit Differentiation

Example Question #104 : Chain Rule And Implicit Differentiation

Example Question #201 : Computation Of The Derivative

Example Question #101 : Chain Rule And Implicit Differentiation

Example Question #102 : Chain Rule And Implicit Differentiation

Example Question #1 : Interpretations And Properties Of Definite Integrals

Example Question #1 : Interpretations And Properties Of Definite Integrals

Example Question #1 : Interpretations And Properties Of Definite Integrals

Example Question #3 : Interpretations And Properties Of Definite Integrals

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: