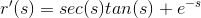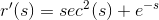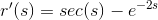We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #91 : Chain Rule And Implicit Differentiation

Find the derivative of the function:

$r(s)=tan(s)-e^{-s}$

Possible Answers:

$r'(s)=sec(s)-e^{-2s}$

$r'(s)=sec(s)tan(s)+e^{-s}$

$r'(s)=sec(s)+e^{-s}$

$r'(s)=sec^2(s)+e^{-s}$

$r'(s)=sec^2(s)-e^{-s}$

Correct answer:

$r'(s)=sec^2(s)+e^{-s}$

Explanation:

*****************************************************************

REQUIRED KNOWLEDGE

*****************************************************************

This problem requires us to understand two things:

1) The derivative of the function $e^{x}$ is always $e^{x}$ by itself

2) By adding an operation to the variable in the exponent (in our case, the -s instead of just s), we must multiply the derivative by the derivative of the argument in the exponent. This is an application of the chain rule of derivation

*****************************************************************

SOLUTION STEPS

***************************************************************** $r(s)=tan(s)-e^{-s}$ is given

Thus:

$r'(s)=\frac{dr}{ds}(tan(s)-e^{-s})$

$r'(s)=\frac{dr}{ds}(tan(s))-\frac{dr}{ds}(e^{-s})$

$r'(s)=sec^2(s)-{\color{Red} (-1)}e^{-s}$ The -1 comes from the derivative of -s

Thus, the correct answer is:

*****************************************************************

CORRECT ANSWER

*****************************************************************

$r'(s)=sec^2(s)+e^{-s}$

*****************************************************************

PROBLEMS?

*****************************************************************

If you did not understand the concepts required to solve this derivative problem:

Look into the derivative of e raised to an argument
Practice applying the chain rule to derivative problems

Report an Error

Example Question #92 : Chain Rule And Implicit Differentiation

Find the derivative of the function:

y=ln(sin^2(x))

Possible Answers:

$y'=\frac{2sin(x)}{cos(x)}$

$y'=-\frac{2sin(x)}{cos(x)}$

$y'=-\frac{2cos(x)}{sin(x)}$

$y'=\frac{2cos(x)}{sin(x)}$

$y'=\frac{cos(x)}{sin(x)}$

Correct answer:

$y'=\frac{2cos(x)}{sin(x)}$

Explanation:

*****************************************************************

STEPS

*****************************************************************

Given:

y=ln(sin^2(x))

Let:

sin^2(x)=x

Now:

y=ln(x)

$y'=\frac{1}{x}*(chain)$

Now, we plug in sin^2(x) again

$y'=\frac{1}{sin^2(x)}*(chain)$

To find "chain", we must take the derivative of sin^2(x), using the product rule:

d(sin^2(x))=d(sin(x)*sin(x))

d(sin^2(x))=sin(x)cos(x)+sin(x)cos(x)

chain=d(sin^2(x))=2sin(x)cos(x)

Plug in this new-found term into the chain in the above derivative:

$y'=\frac{1}{sin^2(x)}*(chain)$

$y'=\frac{1}{sin^2(x)}*(2sin(x)cos(x))$

$y'=\frac{2sin(x)cos(x)}{sin^2(x)}$

Canceling the sin on top with a sin on bottom, we arrive at the correct answer:

*****************************************************************

CORRECT ANSWER

*****************************************************************

${\color{Red} y'=\frac{2cos(x)}{sin(x)}}$

Report an Error

Example Question #93 : Chain Rule And Implicit Differentiation

Given:

y=8x , $\frac{dx}{dt}=3$

Find:

$\frac{dy}{dt}$

Possible Answers:

$\frac{dy}{dt}=\frac{1}{12}$

$\frac{dy}{dt}=24$

$\frac{dy}{dt}=-24$

$\frac{dy}{dt}=12$

$\frac{dy}{dt}=-12$

Correct answer:

$\frac{dy}{dt}=24$

Explanation:

*****************************************************************

STEPS

*****************************************************************

Understand that if:

y=8x ,

then:

$\frac{dy}{dx}=8$

Rearrange this as such:

dy=8dx

We are also given:

$\frac{dx}{dt}=3$

Thus,

dx=3dt

Plugging in 3dt into our previous dx allows us to look for dy/dt

dy=8dx

dy=8(3dt)

dy=24dt

Rearranging, we arrive at the correct answer:

*****************************************************************

CORRECT ANSWER

*****************************************************************

${\color{Red} \frac{dy}{dt}=24}$

Report an Error

Example Question #93 : Chain Rule And Implicit Differentiation

Find the derivative of the function:

$g(x)=sin^{-1}(x^3)$

Possible Answers:

$g'(x)=\frac{3x^2}{\sqrt{1-x^6}}$

$g'(x)=-\frac{3x^2}{\sqrt{1-x^2}}$

$g'(x)=-\frac{x^2}{\sqrt{1-3x^2}}$

$g'(x)=\frac{x^2}{\sqrt{1-3x^2sin(x)}}$

$g'(x)=-\frac{3x^2}{\sqrt{1-x^6}}$

Correct answer:

$g'(x)=\frac{3x^2}{\sqrt{1-x^6}}$

Explanation:

*****************************************************************

STEPS

*****************************************************************

Given:

$g(x)=sin^{-1}(x^3)$

Implement the sin^-1 derivative:

$g'(x)=\frac{1}{\sqrt{1-{\color{Green} (x^3)}^2}}*{\color{Blue} (chain)}$

Understand that we find our chained term by deriving the compound element(in this case, x^3)

${\color{Blue} d(x^3)=3x^2}$

Plug our new-found element in for the chain, and multiply accordingly:

$g'(x)=\frac{1}{\sqrt{1- (x^6)}}*{\color{Blue} (3x^2)}$

After multiplying, we arrive at the correct answer:

*****************************************************************

ANSWER

*****************************************************************

${\color{Red} g'(x)=\frac{3x^2}{\sqrt{1-x^6}}}$

Report an Error

Example Question #271 : Derivatives

Find the derivative of the function:

$s(r)=tan^{-1}(1-r^2)$

Possible Answers:

$s'(r)=\frac{2r^2}{2+1+2r^2}$

$s'(r)=\frac{-2r}{1+(1-r^2)^2}$

$s'(r)=-\frac{4r^2}{3r+2r^2}$

$s'(r)=\frac{2r}{2+(1-2r^2)^2}$

$s'(r)=\frac{4r^2}{3r+2r^2}$

Correct answer:

$s'(r)=\frac{-2r}{1+(1-r^2)^2}$

Explanation:

*****************************************************************

STEPS

*****************************************************************

Given:

$s(r)=tan^{-1}(1-r^2)$

Apply the derivative of arc-tangent (tan^-1)

$s'(r)=\frac{1}{1+(1-r^2)^2}*{\color{Blue} (chain)}$

Understand that to find the (chain term), we must derive the compound function element, in this case it is (1-r^2)

${\color{Blue} (chain)=d(1-r^2)=-2r}$

Now, we plug -2r in for the chain term

$s'(r)=\frac{1}{1+(1-r^2)^2}*{\color{Blue} -2r}$

Multiplying it across, we arrive at the final, correct answer:

*****************************************************************

ANSWER

*****************************************************************

${\color{Red} s'(r)=\frac{-2r}{1+(1-r^2)^2}}$

Report an Error

Example Question #95 : Chain Rule And Implicit Differentiation

Find f'(x) :

$f(x)=\gamma e^{x^2}$ , where $\gamma$ is a function of x.

Possible Answers:

$e^{x^2}\frac{\mathrm{d} \gamma}{\mathrm{d} x} + 2x\gamma e^{x^2}$

$2x\gamma e^{x^2}$

$e^{x^2} (2x\gamma+1)$

$e^{x^2}\frac{\mathrm{d} \gamma}{\mathrm{d} x}$

Correct answer:

$e^{x^2}\frac{\mathrm{d} \gamma}{\mathrm{d} x} + 2x\gamma e^{x^2}$

Explanation:

The derivative of the function is equal to

$f'(x)=e^{x^2}\frac{\mathrm{d} \gamma}{\mathrm{d} x} + 2x\gamma e^{x^2}$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} e^x=e^x$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Note that because $\gamma$ is a function of x, when we use the product rule, we must include its derivative.

Report an Error

Example Question #272 : Derivatives

Calculate the derivative of (x+e^x)^3 .

Possible Answers:

(x+e^x)^2(1+e^x)

(1+e^x)

3e^x(x+e^x)^2

3(x+e^x)^2(1+e^x)

3(x+e^x)^2

Correct answer:

3(x+e^x)^2(1+e^x)

Explanation:

We know how to take the derivative of x^3 , but not (x+e^x)^3 , so let's use the chain rule.

According to the chain rule, we should take the derivative of the outside function and multiply it by the derivative of the inside function. This gives us:

$(x+e^x)^3\rightarrow 3(x+e^x)^2 * (1+e^x)$

Remember that (e^x)'=e^x .

Our final answer:

3(x+e^x)^2(1+e^x)

Report an Error

Example Question #101 : Chain Rule And Implicit Differentiation

Find the derivative of $\ln x^5$ .

Possible Answers:

$\frac{5x^4}{x}$

$5 \ln x^4$

$\frac{1}{x}$

$\frac{5}{x}$

$\frac{1}{x^5}$

Correct answer:

$\frac{5}{x}$

Explanation:

There are two ways to do this problem.

Method 1: Use the power rule to turn $\ln x^5$ into $5\ln x$ , the derivative of which is $\tfrac{5}{x}$ .

Method 2: Use the chain rule.

$(\ln x^5)'=(\tfrac{1}{x^5})(5x^4)=\tfrac{5}{x}$

Either way, the answer is $\frac{5}{x}$ .

Report an Error

Example Question #101 : Chain Rule And Implicit Differentiation

Find the derivative of $e^{x^2}$ .

Possible Answers:

$xe^{x^2}$

$2xe^{x^2}$

2e^x

$2e^{x^2}$

$e^{x^2}$

Correct answer:

$2xe^{x^2}$

Explanation:

Using the chain rule (f(g))'=f'(g)*g' :

$(e^{x^2})'=(e^{x^2})(2x)=2xe^{x^2}$

Report an Error

Example Question #192 : Computation Of The Derivative

Find the derivative of $\tan(xe^x)$ .

Possible Answers:

$(xe^x)\sec^2 (x)$

$e^x\sec^2 (e^x)$

$(xe^x+e^x)\sec^2 (xe^x)$

$e^x\sec^2 (xe^x)$

$\sec^2 (xe^x)$

Correct answer:

$(xe^x+e^x)\sec^2 (xe^x)$

Explanation:

First, use the chain rule (f(g))'=f'(g)*g' :

$(\tan(xe^x))'=sec^2(xe^x)*(xe^x)'$

Now we have to use the product rule (fg)'=fg'+gf'

(xe^x)'=xe^x+e^x(1)

Our final answer:

$(xe^x+e^x)\sec^2 (xe^x)$

Report an Error

View AP Calculus AB Tutors

MrG
Certified Tutor

Long Island University-Brooklyn Campus, Master of Science, Applied Mathematics.

View AP Calculus AB Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View AP Calculus AB Tutors

Emily
Certified Tutor

University of Michigan-Ann Arbor, Bachelor of Science, Public Health.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in San Francisco-Bay Area, Physics Tutors in San Diego, SAT Tutors in Houston, GRE Tutors in Phoenix, ACT Tutors in Atlanta, ISEE Tutors in San Francisco-Bay Area, GMAT Tutors in Boston, Spanish Tutors in Los Angeles, SSAT Tutors in Philadelphia, Calculus Tutors in Los Angeles

Popular Courses & Classes

SAT Courses & Classes in Washington DC, SAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in Houston, SAT Courses & Classes in Seattle, SAT Courses & Classes in Atlanta, LSAT Courses & Classes in Phoenix, ACT Courses & Classes in Philadelphia, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Philadelphia

Popular Test Prep

ACT Test Prep in Houston, ISEE Test Prep in Washington DC, ISEE Test Prep in Phoenix, ISEE Test Prep in Seattle, GMAT Test Prep in New York City, GRE Test Prep in Phoenix, ACT Test Prep in Phoenix, ISEE Test Prep in Philadelphia, SSAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #91 : Chain Rule And Implicit Differentiation

Example Question #92 : Chain Rule And Implicit Differentiation

Example Question #93 : Chain Rule And Implicit Differentiation

Example Question #93 : Chain Rule And Implicit Differentiation

Example Question #271 : Derivatives

Example Question #95 : Chain Rule And Implicit Differentiation

Example Question #272 : Derivatives

Example Question #101 : Chain Rule And Implicit Differentiation

Example Question #101 : Chain Rule And Implicit Differentiation

Example Question #192 : Computation Of The Derivative

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: