All AP Calculus AB Resources
Example Questions
Example Question #234 : Derivatives
A reaction is modeled by the following equation:
where 
What is 
The derivative of the function is equal to
and was found using the following rules:


The chain rule was used for the function contained in the exponential function (or, as written as a rule, 
Example Question #235 : Derivatives
For the equation, 

The equation given is not written and 



"With respect to 



First we must differentiate both sides with respect to 
We have multiple terms on the left hand side, so we will differentiate each term individually.
For the first term, ![\frac{\mathrm{d} }{\mathrm{d} x}[y^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967672/gif.latex)

The blue part is the power rule. The red is from the chain rule. The red part is the derivative of y with respect to x, which is currently unknown. Remember that y is some unknown function of x, whose derivative is also unknown. We can only write 
Now we find the second term's derivative,
This is a product rule. To help with the product rule, the two pieces are color coded. Remember that the power rule is
Applying this, we get
Simplifying gives us
For the third term, 

remember that the derivative of 


The right hand side of the equation is a constant, so its derivative is zero.
Assembling all the parts back together, we have
Now that we have differentiated the equation, we need to algebraically solve for 
First, we should move all terms with a 

Then we will will factor out the common factor of 
Then, to isolate 
![[2y + 2x^2 + 5xy^{-2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969713/gif.latex)
Now we need to simplify and get rid of the negative exponents. To do this, we can simply multiply the numerator and denominator by 
Which is the correct answer.
Example Question #236 : Derivatives
Given the function 
Given the function 
where 




Example Question #237 : Derivatives
Given the function 
Given the function 
where 




Example Question #238 : Derivatives
Given the function 
Given the function 
where 




Example Question #51 : Chain Rule And Implicit Differentiation
Given the function 
Given the function 
where 




Example Question #240 : Derivatives
Given the function 
Given the function 
where 




Example Question #241 : Derivatives
Given the function 
Given the function 
where 




Example Question #242 : Derivatives
Given the function 
Given the function 
where 




Example Question #243 : Derivatives
Given the function 
Given the function 
where 




All AP Calculus AB Resources












![\frac{\mathrm{d} }{\mathrm{d} x}[y^2 + 2x^2y - \frac{5x}{y}] = \frac{\mathrm{d} }{\mathrm{d} x}[2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967670/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[y^2] + \frac{\mathrm{d} }{\mathrm{d} x}[2x^2y] + \frac{\mathrm{d} }{\mathrm{d} x}[\frac{-5x}{y}] = \frac{\mathrm{d} }{\mathrm{d} x}[2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969699/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[y^2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967674/gif.latex)
![{\color{Blue} 2[y]^{2-1}}{\color{DarkRed} (\frac{\mathrm{d} y}{\mathrm{d} x})}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967675/gif.latex)

![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} 2x^2}{\color{DarkRed} y}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967678/gif.latex)
![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} f(x)}\cdot{\color{DarkRed} g(x)}] ={\color{Blue} f(x)}\cdot {\color{DarkRed} g'(x)} + {\color{Blue} f'(x)} \cdot {\color{DarkRed} g(x)}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/967679/gif.latex)


![\frac{\mathrm{d} }{\mathrm{d} x}[{\color{Blue} -5x}{\color{DarkRed} y^{-1}}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969702/gif.latex)




![\frac{\mathrm{d} y}{\mathrm{d} x}[2y + 2x^2 + 5xy^{-2}] = -4xy + 5y^{-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969711/gif.latex)



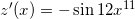



![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970854/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971039/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971030/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971052/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970993/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971070/gif.latex)





![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971096/gif.latex)
![\small \small \small \small z'(x)=[-\sin (5-x^{10})][-10x^9]=10x^{9}\sin(5-x^{10})](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971102/gif.latex)




![\small [f(g(x))]'=f'(g(x))g'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/971087/gif.latex)




