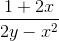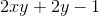We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #441 : Ap Calculus Ab

Find the derivative of the following function:

sin(tanx) .

Possible Answers:

cos(sec^2x)

-cos(tanx)

sec^2xcos(tanx)

cos(tanx)

sin(sec^2x)

Correct answer:

sec^2xcos(tanx)

Explanation:

For a chain rule derivative, we take the derivative of the outside function (leaving the inside function unchanged). Then, you multiply that by the derivative of the inside.

sin(tanx)'=sin'(tanx)*tanx'=cos(tanx)*sec^2x

=sec^2xcos(tanx).

Report an Error

Example Question #442 : Ap Calculus Ab

Find the derivative of the following function:

f(x)=ln(3x^7) .

Possible Answers:

21x^6ln(3x^7)

$\frac{3}{x^7}$

$\frac{3}{x}$

$\frac{7}{x}$

$\frac{1}{3x^7}$

Correct answer:

$\frac{7}{x}$

Explanation:

For a chain rule derivative, we need to take the derivative of lnx first. Then, we multiply by the derivative of the inside function. In other words, the general chain derivative of the function is:

$ln(u)'=\frac{u'}{u}.$

$ln(3x^7)=\frac{21x^6}{3x^7}=\frac{7}{x}.$

Report an Error

Example Question #443 : Ap Calculus Ab

Find the derivative of the following function:

$e^{cotx}$ .

Possible Answers:

$-sec^2xe^{cotx}$

$csc^2xe^{cotx}$

$e^{-csc^2x}$

$-csc^2xe^{cotx}$

$sec^2xe^{cotx}$

Correct answer:

$-csc^2xe^{cotx}$

Explanation:

The exponential function is the only derivative that always returns the original function. Therefore, we only need to multiply that by the derivative of the new exponent.

e^u'=e^u*u' .

$e^{cotx}'=e^{cotx}*-csc^2x=-csc^2xe^{cotx}.$

Report an Error

Example Question #444 : Ap Calculus Ab

Find the derivative of the following function:

$\sqrt{1-sin^2x}$ .

Possible Answers:

cos(x)

-cos(x)

-sin(x)

sin(x)

$\frac{1}{2\sqrt{1-sin^2x}}$

Correct answer:

-sin(x)

Explanation:

Here, we need to take the derivative of a square root function first. Then, we will multiply that by the derivative of the function under the square root.

$\sqrt{1-sin^2x}'=\frac{1}{2\sqrt{1-sin^2x}}*-2sinx*cosx.$

Remember: -sin^2x'=-2sinx*cosx by another chain rule.

Now, let's make use of our trigonometric identities:

$sin^2x+cos^2x=1. \; 1-sin^2x=cos^2x$

Therefore, we can simplify our answer:

$\frac{-2sinxcosx}{2\sqrt{cos^2x}}=\frac{-sinxcosx}{cosx}=-sinx.$

Note, you could have used this trigonometric identity from the very beginning, making the problem much easier!

Report an Error

Example Question #42 : Chain Rule And Implicit Differentiation

Find $\frac{dy}{dx}.$

x^2+3y-sinx=2.

Possible Answers:

$\frac{dy}{dx}=\frac{2-cosx-2x}{3}$

$\frac{dy}{dx}=\frac{cosx-2x}{3}$

$\frac{dy}{dx}=\frac{-cosx-2x}{3}$

$\frac{dy}{dx}=\frac{2+cosx-2x}{3}$

$\frac{dy}{dx}=cosx-2x$

Correct answer:

$\frac{dy}{dx}=\frac{cosx-2x}{3}$

Explanation:

For implicit differentiation, we need to take a derivative from left to right of our function. The only difference is that any time we take the derivative of a function, we need to explicitly write $\frac{dy}{dx}$ after it. Then, we will use algebra to solve for that $\frac{dy}{dx}.$

$(x^2+3y-sinx=2)'=2x+3\frac{dy}{dx}-cosx=0.$

$\frac{dy}{dx}=\frac{cosx-2x}{3}.$ Here, just move everything other than the term we want to the right. Then, divide by the coefficient.

Report an Error

Example Question #43 : Chain Rule And Implicit Differentiation

Find $\frac{dy}{dx}$ for the following function:

x^3-2y^2+3x=4

Possible Answers:

$\frac{dy}{dx}=\frac{3-3x^2}{4}$

$\frac{dy}{dx}=\frac{3-3x^2}{2y^2}$

$\frac{dy}{dx}=\frac{3+3x^2}{4y}$

$\frac{dy}{dx}=\frac{3+3x^2}{2y^2}$

$\frac{dy}{dx}=\frac{3+3x^2}{4}$

Correct answer:

$\frac{dy}{dx}=\frac{3+3x^2}{4y}$

Explanation:

For implicit differentiation, we need to take the derivative of every term, including numbers. Whenever we take a derivative of a function of , we need to multiply it by $\frac{dy}{dx}$ . Then, we will rearrange the equation to solve for $\frac{dy}{dx}.$

$(x^3-2y^2+3x=4)'=3x^2-4y\frac{dy}{dx}+3=0$

$\frac{dy}{dx}=\frac{-3x^2-3}{-4y}=\frac{3x^2+3}{4y}.$

In the last step, I canceled all of the negative signs.

Report an Error

Example Question #141 : Computation Of The Derivative

Determine the derivative of $f(x)=2\tan ^2(x^2)$

Possible Answers:

$4x\tan(x^2)$

$8x\tan(x^2)\sec^2(x^2)$

$8x\sec^2(x^2)$

$4\tan(x^2)\sec^2(x^2)$

$4x\sec^2(x^2)$

Correct answer:

$8x\tan(x^2)\sec^2(x^2)$

Explanation:

This is a pure problem on understanding how chain rules work for derivatives.

First thing we need to remember is that the derivative of $\tan(x)$ is $\sec^2(x)$ .

When we are taking the derivative of $f(x)=2\tan ^2(x^2)$ , we can first pull out the 2 in the front and we treat $\tan^2(x^2)$ as $[\tan(x^2)]^2$ .

This way, the derivative will become $2*2*\tan(x^2)*\frac{\mathrm{d} tan(x^2)}{\mathrm{d} x}$ ,

which is $4\tan(x^2)*(2x\sec(x^2))$ .

Report an Error

Example Question #231 : Derivatives

Find $\frac{\mathrm{d}y }{\mathrm{d} x}$ of the following equation:

x^2y+y^2=x

Possible Answers:

$\frac{1+2x}{2y-x^2}$

2xy+2y-1

x^2+2y

$\frac{1+2x}{2y+x^2}$

$\frac{1-2x}{2y+x^2}$

Correct answer:

$\frac{1-2x}{2y+x^2}$

Explanation:

To find $\frac{\mathrm{d}y }{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.

Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$2x+x^2\frac{\mathrm{d} y}{\mathrm{d} x}+2y\frac{\mathrm{d} y}{\mathrm{d} x}=1$

using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x}ax=a$

Note that for every derivative of a function with y, the additional term $\frac{\mathrm{d} y}{\mathrm{d} x}$ appears; this is because of the chain rule, where y = g(x) , so to speak, for the function it appears in.

Using algebra to rearrange, we get

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1-2x}{2y+x^2}$

Report an Error

Example Question #141 : Computation Of The Derivative

Find the derivative:

$f(x)=\sqrt{e^\tan(x^2)}$

Possible Answers:

$x\sec^2(x^2)\sqrt{e^\tan(x^2)}$

$\frac{x\sec^2(x^2)}{\sqrt{e^{\tan^{(x^2)}}}}$

$\frac{2x\sec^2(x^2)}{\sqrt{e^{\tan^{(x^2)}}}}$

$\frac{x\sec^2(x^2)\sqrt{e^{\tan(x^2)}}}{2}$

Correct answer:

$x\sec^2(x^2)\sqrt{e^\tan(x^2)}$

Explanation:

The derivative of the function is equal to

$f'(x)=x\sec^2(x^2)\sqrt{e^\tan(x^2)}$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} e^u=e^u\frac{\mathrm{d} u}{\mathrm{d} x}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \tan(x)=\sec^2(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Before simplification, the derivative we get is

$f'(x)=\frac{e^{\tan(x^2)^{-\frac{1}{2}}}}{2}(2x\sec^2(x^2)e^{\tan(x^2)})$

Note that the square root, the exponential, and the tangent function all utilize chain rule when taking their derivatives.

Report an Error

Example Question #446 : Ap Calculus Ab

Find the first derivative of the following function:

$f=\cos(e^{2x})$

Possible Answers:

$2e^{2x}\sin(e^{2x})$

$-e^{2x}\sin(e^{2x})$

$-2e^{2x}\sin(e^{2x})$

$-\sin(e^{2x})$

Correct answer:

$-2e^{2x}\sin(e^{2x})$

Explanation:

The derivative of the function is equal to

$f'=-2e^{2x}\sin(e^{2x})$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \cos(x)=-\sin(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} e^x=e^x$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Note that the first rule - the chain rule - was used three times for the function: the cosine, contained the exponential which itself was raised to a function. (Note that sometimes the exponential rule is written as $\frac{\mathrm{d} }{\mathrm{d} x} e^u=e^u \frac{\mathrm{d} u}{\mathrm{d} x}$ , which itself is the chain rule.)

Report an Error

View AP Calculus AB Tutors

Madeline
Certified Tutor

University of Central Florida, Current Undergrad, Physics.

View AP Calculus AB Tutors

Dalton
Certified Tutor

University of Massachusetts Amherst, Doctor of Philosophy, Mathematics.

View AP Calculus AB Tutors

Fathima
Certified Tutor

BITS Pilani Goa, Doctorate (PhD), Mathematics.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Chicago, GRE Tutors in Chicago, GRE Tutors in Phoenix, Spanish Tutors in Washington DC, GMAT Tutors in Dallas Fort Worth, Spanish Tutors in San Diego, SSAT Tutors in Dallas Fort Worth, Math Tutors in Philadelphia, ISEE Tutors in Chicago, ACT Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Washington DC, SSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Denver, Spanish Courses & Classes in Philadelphia, GMAT Courses & Classes in Houston, MCAT Courses & Classes in Washington DC, MCAT Courses & Classes in Denver, GMAT Courses & Classes in San Diego, ACT Courses & Classes in New York City

Popular Test Prep

LSAT Test Prep in Phoenix, GMAT Test Prep in Philadelphia, SAT Test Prep in San Diego, SAT Test Prep in Denver, ACT Test Prep in New York City, SSAT Test Prep in Denver, MCAT Test Prep in Boston, GMAT Test Prep in Houston, GRE Test Prep in Washington DC, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #441 : Ap Calculus Ab

Example Question #442 : Ap Calculus Ab

Example Question #443 : Ap Calculus Ab

Example Question #444 : Ap Calculus Ab

Example Question #42 : Chain Rule And Implicit Differentiation

Example Question #43 : Chain Rule And Implicit Differentiation

Example Question #141 : Computation Of The Derivative

Example Question #231 : Derivatives

Example Question #141 : Computation Of The Derivative

Example Question #446 : Ap Calculus Ab

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: