Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int (4x^7+x^4+x)dx$

Possible Answers:

$\frac{1}{2}x^8+\frac{1}{5}x^5+\frac{1}{2}x^2+C$

x^8+x^5+x^2+C

${2}x^8+{5}x^5+{2}x^2+C$

$\frac{1}{7}x^7+\frac{1}{4}x^4+x+C$

$\frac{1}{2}x^8+\frac{1}{5}x^4+\frac{1}{2}x^2$

Correct answer:

$\frac{1}{2}x^8+\frac{1}{5}x^5+\frac{1}{2}x^2+C$

Explanation:

Use the inverse Power Rule to evaluate the integral. We know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . We see that this rule tells us to increase the power of by 1 and multiply by $\frac{1}{n+1}$ . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #3 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int 3y dy$

Possible Answers:

3y+C

$\frac{1}{3}y^2+C$

3y^2+C

$\frac{1}{2}y^2+C$

$\frac{3}{2}y^2+C$

Correct answer:

$\frac{3}{2}y^2+C$

Explanation:

Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of integrals, so we pull the 3 out front. Next, according to the inverse power rule, we know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . We see that this rule tells us to increase the power of by 1 and multiply by $\frac{1}{n+1}$ . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #5 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int (x-2x^3+1)dx$

Possible Answers:

$\frac{1}{2}x^2+\frac{1}{2}x^4+x+C$

2x^2-4x^4+x+C

$\frac{1}{3}x^3-\frac{3}{2}x^2+C$

2x^2-2x^4+x+C

$\frac{1}{2}x^2-\frac{1}{2}x^4+x+C$

Correct answer:

$\frac{1}{2}x^2-\frac{1}{2}x^4+x+C$

Explanation:

Report an Error

Example Question #6 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int (1-x)dx$

Possible Answers:

x+x^2+C

x-x^2+C

$x+\frac{1}{2}x^2+C$

$x-\frac{1}{2}x^2+C$

x+2x^2+C

Correct answer:

$x-\frac{1}{2}x^2+C$

Explanation:

Use the inverse Power Rule to evaluate the integral. We know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . We see that this rule tells us to increase the power of by 1 and multiply by $\frac{1}{n+1}$ Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #7 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int \frac{1}{2}xdx$

Possible Answers:

2x^2+C

$\frac{1}{2}x+C$

4x^2+C

$\frac{1}{4}x^2+C$

$\frac{1}{2}x^2+C$

Correct answer:

$\frac{1}{4}x^2+C$

Explanation:

Use the inverse Power Rule to evaluate the integral. Firstly, constants can be taken out of the integral, so we pull the 1/2 out front and then complete the integration according to the rule. We know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . We see that this rule tells us to increase the power of by 1 and multiply by $\frac{1}{n+1}$ . Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #241 : Ap Calculus Ab

Evaluate the following indefinite integral.

$\int \frac{1}{x}dx$

Possible Answers:

x+C

ln|x|+C

e^x+C

1+C

Correct answer:

ln|x|+C

Explanation:

Use the inverse Power Rule to evaluate the integral. We know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . But, in this case, IS equal to so a special condition of the rule applies. We must instead use $\int x^{-1}dx=ln|x|+C$ . Evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #11 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following indefinite integral.

$\int \frac{3}{x}dx$

Possible Answers:

ln|x|+C

$\frac{3}{2}x^3+C$

3ln|x|+C

3e^x+C

$\frac{1}{3}ln|x|+C$

Correct answer:

3ln|x|+C

Explanation:

Use the inverse Power Rule to evaluate the integral. We know that $\int x^n dx= \frac{x^{n+1}}{n+1}+C$ for $n \ne -1$ . But, in this case, IS equal to so a special condition of the rule applies. We must instead use $\int x^{-1}dx=ln|x|+C$ . Pull the constant "3" out front and evaluate accordingly. Next always add your constant of integration that would be lost in the differentiation. Take the derivative of your answer to check your work.

Report an Error

Example Question #12 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Evaluate the following definite integral.

$\int_{0}^{2}(x^2+3) dx$

Possible Answers:

5/3

3x^3+6x

$\frac{1}{3}x^3+3x+C$

26/3

Correct answer:

26/3

Explanation:

Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 0 to 2. First, we use our inverse power rule to find the antiderivative. So, we have that 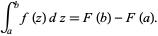$\int x^ndx=\frac{x^{n+1}}{n+1}$ . Once you find the antiderivative, we must remember that int_a^bf(z)dz=F(b)-F(a). where is the indefinite integral. So, we plug in our limits and subtract the two. So, we have $(\frac{1}{3}x^3+3x)|_0^2=[\frac{1}{3}2^3+3(2)]-[\frac{1}{3}0^3+3(0)]=26/3$ .

Report an Error

Example Question #41 : Functions, Graphs, And Limits

Evaluate the following definite integral.

$\int_{1}^{3}6xdx$

Possible Answers:

6x^2

3x^2+C

Correct answer:

Explanation:

Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 3. First, we use our inverse power rule to find the antiderivative. So, we have that 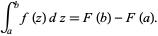$\int x^ndx=\frac{x^{n+1}}{n+1}$ . Once you find the antiderivative, we must remember that int_a^bf(z)dz=F(b)-F(a). where is the indefinite integral. So, we plug in our limits and subtract the two. So, we have (3x^2)|_1^3=3(3^2)-3(1^2)=24 .

Report an Error

Example Question #42 : Functions, Graphs, And Limits

Evaluate the following definite integral.

$\int_{1}^{4}\frac{1}{x}dx$

Possible Answers:

2x^2

$ln\ 4$

$ln\ 1$

$ln\ 3$

Correct answer:

$ln\ 4$

Explanation:

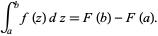Unlike an indefinite integral, the definite integral must be evaluated at its limits, in this case, from 1 to 4. First, we use our inverse power rule to find the antiderivative. So since is to the power of , we have that $\int x^{-1}=ln|x|$ . Once you find the antiderivative, we must remember that int_a^bf(z)dz=F(b)-F(a). where is the indefinite integral. So, we plug in our limits and subtract the two. So, we have ln(x)|_1^4=ln(4)-ln(1)=ln(4) because we know that $ln\ 1=0$ .

Report an Error

View AP Calculus AB Tutors

Varun
Certified Tutor

University of Arizona, Bachelor of Science, Aerospace Engineering.

View AP Calculus AB Tutors

Jeremy
Certified Tutor

University of Illinois at Chicago, Bachelor of Science, Physics.

View AP Calculus AB Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Boston, French Tutors in Houston, English Tutors in Denver, Chemistry Tutors in Los Angeles, Reading Tutors in San Diego, SAT Tutors in San Francisco-Bay Area, Chemistry Tutors in Boston, Math Tutors in Boston, Algebra Tutors in Phoenix, ACT Tutors in Miami

Popular Courses & Classes

LSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Los Angeles, ISEE Courses & Classes in Seattle, LSAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Washington DC, MCAT Courses & Classes in Seattle, SAT Courses & Classes in Denver, ACT Courses & Classes in Houston, LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Houston

Popular Test Prep

GRE Test Prep in San Diego, MCAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Philadelphia, GRE Test Prep in Phoenix, SAT Test Prep in Philadelphia, GRE Test Prep in Los Angeles, LSAT Test Prep in New York City, ISEE Test Prep in Houston, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #3 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #3 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #5 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #6 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #7 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #241 : Ap Calculus Ab

Example Question #11 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #12 : Comparing Relative Magnitudes Of Functions And Their Rates Of Change

Example Question #41 : Functions, Graphs, And Limits

Example Question #42 : Functions, Graphs, And Limits

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: