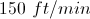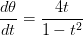Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Derivatives

The speed of a car traveling on the highway is given by the following function of time:

v(t) = 5t^2+2t

Note that

v(0) =0

What does this mean?

Possible Answers:

The car's speed is constantly changing at time t=0 .

The car takes seconds to reach its maximum speed.

The car is not accelerating at time t=0 .

The car is not moving at time t=0 .

The car is not decelerating at time t=0 .

Correct answer:

The car is not moving at time t=0 .

Explanation:

The function v(t) gives you the car's speed at time . Therefore, the fact that v(0)=0 means that the car's speed is at time . This is equivalent to saying that the car is not moving at time t=0 . We have to take the derivative of to make claims about the acceleration.

Report an Error

Example Question #3 : Techniques Of Antidifferentiation

A jogger leaves City at t=0 . His subsequent position, in feet, is given by the function:

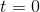
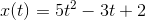
$x(t) = 5t^{2} - 3t + 2$ ,

where is the time in minutes.

Find the velocity of the jogger at 15 minutes.

Possible Answers:

$147\ ft/min$

$147\ ft$

$150\ ft/min$

$372\ ft/min$

$120\ ft/min$

Correct answer:

$147\ ft/min$

Explanation:

To find velocity, one has to use the first derivative of f(t) :

v(t) = x'(t) = 10t - 3 .

v(15) = 10(15) - 3 = 147 ft/min.

Note the units have to be ft/min.

Report an Error

Example Question #161 : Derivatives

A gun sends a bullet straight up with a launch velocity of 220 ft/s. It reaches a height of $s=220t-16t^2$ after seconds. What's the acceleration in $m/s^{2}$ of the block after it has been ejected?

Possible Answers:

Correct answer:

Explanation:

Since $a=\frac{ds^2}{dt^2}$ , by differentiating the position function twice, we see that acceleration is constant and $-32\ m/s^{2}$ . Acceleration, in this case, is gravity, which makes sense that it should be a constant value!

Report an Error

Example Question #162 : Derivatives

The speed of a car traveling on the highway is given by the following function of time:

f(t) = 5t^2+2t

Consider a second function:

g(t) = 10t+2

What can we conclude about this second function?

Possible Answers:

It represents the rate at which the speed of the car is changing.

It represents the total distance the car has traveled at time .

It represents another way to write the car's speed.

It has no relation to the previous function.

It represents the change in distance over a given time .

Correct answer:

It represents the rate at which the speed of the car is changing.

Explanation:

Notice that the function g(t) is simply the derivative of f(t) with respect to time. To see this, simply use the power rule on each of the two terms.

f'(t) = (2)(5)t + 2 = g(t)

Therefore, g(t) is the rate at which the car's speed changes, a quantity called acceleration.

Report an Error

Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Find the critical numbers of the function,

$f(x)=\frac{1+x^2}{x}$

Possible Answers:

$x =\left \{ -1,0,1\right \}$

$x =\left \{ -1\right \}$

$x =\left \{ 1\right \}$

$x =\left \{ -1,1\right \}$

Correct answer:

$x =\left \{ -1,1\right \}$

Explanation:

$f(x)=\frac{1+x^2}{x}$

1) Recall the definition of a critical point:

The critical points of a function f(x) are defined as points (a,f(a)) , such that x=a is in the domain of f(x) , and at which the derivative f'(a) is either zero or does not exist. The number x=a is called a critical number of f(x) .

2) Differentiate ,

$f'(x)=\frac{d}{dx}\left(\frac{1+x^2}{x} \right )=\frac{d}{dx}\left(\frac{1}{x}+x \right )=-\frac{1}{x^2}+1$

3) Set to zero and solve for ,

$f'(x)=-\frac{1}{x^2}+1= 0$

$\frac{1}{x^2}=1$

The critical numbers are,

$x =\left \{ -1,1\right \}$

We can also observe that the derivative does not exist at x = 0 , since the $-\frac{1}{x^2}$ term would be come infinite. However, is not a critical number because the original function f(x) is not defined at x=0 . The original function is infinite at x=0 , and therefore x = 0 is a vertical asymptote of f(x) as can be seen in its' graph,

Problem 7 plot

Further Discussion

In this problem we were asked to obtain the critical numbers. If were were asked to find the critical points, we would simply evaluate the function f(x) at the critical numbers to find the corresponding function values and then write them as a set of ordered pairs,

$\left \{(-1,-2), (1,2) \right \}$

Report an Error

Example Question #2 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

The function f(x) is a continuous, twice-differentiable functuon defined for all real numbers.

If the following are true:

Which function could be f(x) ?

Possible Answers:

sin(x)

e^x

$\frac{1}{x^2}$

ln(x)

Correct answer:

ln(x)

Explanation:

To answer this problem we must first interpret our given conditions:

Implies the function is strictly increasing.
Implies the function is strictly concave down.

We note the only function given which fufills both of these conditions is lnx .

Report an Error

Example Question #3 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

A jogger leaves City at t=0 . His subsequent position, in feet, is given by the function:

$x(t) = 5t^{2} - 3t + 2$ ,

where is the time in minutes.

Find the acceleration of the jogger at t=15 minutes.

Possible Answers:

$10\ ft/min$

$10\ ft/min^{2}$

$10\ ft$

$147\ ft/min^{2}$

$147\ ft/min$

Correct answer:

$10\ ft/min^{2}$

Explanation:

The accelaration is given by the second derivative of the position function:
a(t) = f''(t)

For the given position function:

$f(t) = 5t^{2} - 3t + 2$ ,

f'(t) = 10t - 3 ,

f''(t) = 10 .

Therefore, the acceleration at t=15 minutes is $10\ ft/min^{2}$ . Again, note the units must be in $ft/min^{2}$ .

Report an Error

Example Question #1 : Applications Of Derivatives

A right triangle has sides of lenght and which are both increasing in length over time such that:

x(t)=2t

y(t)=4t^2

a) Find the rate at which the angle $\theta$ opposite y(t) is changing with respect to time.

Possible Answers:

$\frac{d\theta}{dt}=t+\frac{4}{1+2t^2}$

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

$\frac{d\theta}{dt}=\sin(t)+\frac{1}{1+t}$

$\frac{d\theta}{dt}=\frac{4t}{1-t^2}$

$\frac{d\theta}{dt}=\cos(t)-\frac{1}{1+t}$

Correct answer:

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

Explanation:

A right triangle has sides of lenght and which are both increasing in length over time such that:

x(t)=2t

y(t)=4t^2

Find the rate at which the angle $\theta$ opposite y(t) is changing with respect to time.

Quesstion 9 related rates triangle

a) First we need to write an expression for the angle $\theta$ as a function of . Because the angle is opposite the side we know that the tangent is simply y/x . Take the inverse of the tangent:

$\theta (t)\, \, =\, \, \tan^{-1}\left(\frac{y(t)}{x(t)} \right )\: \: =\: \: \tan^{-1}\left(\frac{4t^2}{2t}\right)\, \, =\, \, \tan^{-1}\left(2t \right )$

$\theta(t)=\tan^{-1}(2t)$

Now we need to differentiate with respect to .

Recall the the general derivative for the inverse tangent function is:

$\frac{d}{dx}\tan^{-1}(x)=\frac{1}{1+x^2}$

Applying this to our function for $\theta(t)$ , and remembering to use the chain rule, we obtain:

$\frac{d\theta}{dt}=\frac{d}{dt}\tan^{-1}(2t)=\frac{2}{1+(2t)^2}=\frac{2}{1+4t^2}$

$\frac{d\theta}{dt}=\frac{2}{1+4t^2}$

Report an Error

Example Question #1 : Modeling Rates Of Change, Including Related Rates Problems

Soap is sometimes used to determine the location of leaks in industrial pipes. A perfectly spherical soap bubble is growing at a rate of 5 mm^3/sec . What is the rate of change of the surface area of the bubble when the radius of the bubble is 10 mm ?

Possible Answers:

$\frac{1}{80\pi} mm^2/sec$

1 mm^2/sec

80 mm^2/sec

$80\pi mm^2/sec$

Correct answer:

1 mm^2/sec

Explanation:

To determine the rate of change of the surface area of the spherical bubble, we must relate it to something we do know the rate of change of - the volume.

The volume of a sphere is given by the following:

$V=\frac{4\pi}{3}r^3$

The rate of change of the volume is given by the derivative with respect to time:

$\frac{\mathrm{d} V}{\mathrm{d} t}=4\pi r^2 \frac{\mathrm{d} r}{\mathrm{d} t}$

The derivative was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x)) \cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x}x^n=nx^{n-1}$

We must now solve for the rate of change of the radius at the specified radius, so that we can later solve for the rate of change of surface area:

$5=4\pi (100) \frac{\mathrm{d} r}{\mathrm{d} t}$

$\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{1}{80\pi}$

Next, we must find the surface area and rate of change of the surface area of the sphere the same way as above:

$A=4\pi r^2$

$\frac{\mathrm{d} A}{\mathrm{d} t}=8 \pi r \frac{\mathrm{d} r}{\mathrm{d} t}$

Plugging in the known rate of change of the surface area at the specified radius, and this radius into the rate of surface area change function, we get

$\frac{\mathrm{d} A}{\mathrm{d} t}=8\pi (10)\cdot \frac{1}{80\pi}= 1mm^2/sec$

Report an Error

Example Question #2 : Modeling Rates Of Change, Including Related Rates Problems

A pizzeria chef is flattening a circular piece of dough. The surface area of the dough (we are only considering the top of the dough) is increasing at a rate of 0.5 inches/sec. How quickly is the diameter of the pizza changing when the radius of the pizza measures 4 inches?

Possible Answers:

$\frac{1}{8 \pi}$ inches/sec

inches/sec

$\frac{1}{16 \pi}$ inches/sec

inches/sec

Correct answer:

$\frac{1}{8 \pi}$ inches/sec

Explanation:

To find the rate of change of the diameter, we must relate the diameter to something we do know the rate of change of: the surface area.

The surface area of the top side of the pizza dough is given by

$A=\pi r ^2$

The rate of change, then, is found by taking the derivative of the function with respect to time:

$\frac{\mathrm{d} A}{\mathrm{d} t}=2\pi r \frac{\mathrm{d} r}{\mathrm{d} t}$

Solving for the rate of change of the radius at the given radius, we get

$\frac{1}{2}=2\pi (4)\frac{\mathrm{d} r}{\mathrm{d} t}$

$\frac{\mathrm{d} r}{\mathrm{d} t}=\frac{1}{16\pi}$ inches/sec

Now, we relate the diameter to the radius of the pizza dough:

2r=d

Taking the derivative of both sides with respect to time, we get

$2 \frac{\mathrm{d} r}{\mathrm{d} t}=\frac{\mathrm{d} d}{\mathrm{d} t}$

Plugging in the known rate of change of the radius at the given radius, we get

$\frac{\mathrm{d} d}{\mathrm{d} t}=\frac{1}{8\pi}$ inches/sec

We could have found this directly by writing our surface area formula in terms of diameter, however the process we used is more applicable to problems in which the related rate of change is of something not as easy to manipulate.

Report an Error

View AP Calculus AB Tutors

Riley
Certified Tutor

Reed College, Bachelor in Arts, Mathematics.

View AP Calculus AB Tutors

Aaron
Certified Tutor

Tulsa Community College, Associate in Science, Mechanical Engineering.

View AP Calculus AB Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Washington DC, MCAT Tutors in Dallas Fort Worth, ISEE Tutors in Phoenix, Biology Tutors in Washington DC, ACT Tutors in Boston, Chemistry Tutors in Phoenix, LSAT Tutors in Miami, Algebra Tutors in New York City, French Tutors in Washington DC, SAT Tutors in Miami

Popular Courses & Classes

SAT Courses & Classes in Boston, GMAT Courses & Classes in San Diego, LSAT Courses & Classes in Chicago, MCAT Courses & Classes in New York City, GMAT Courses & Classes in New York City, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Houston, SSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in Seattle, GMAT Test Prep in Atlanta, ACT Test Prep in Seattle, LSAT Test Prep in Phoenix, ISEE Test Prep in New York City, ISEE Test Prep in Houston, ACT Test Prep in Boston, SSAT Test Prep in Miami, GRE Test Prep in Boston, SAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Derivatives

Example Question #3 : Techniques Of Antidifferentiation

Example Question #161 : Derivatives

Example Question #162 : Derivatives

Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #2 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #3 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #1 : Applications Of Derivatives

Example Question #1 : Modeling Rates Of Change, Including Related Rates Problems

Example Question #2 : Modeling Rates Of Change, Including Related Rates Problems

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Derivatives

Example Question #3 : Techniques Of Antidifferentiation

Example Question #161 : Derivatives

Example Question #162 : Derivatives

Example Question #1 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #2 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #3 : Corresponding Characteristics Of Graphs Of ƒ And ƒ'

Example Question #1 : Applications Of Derivatives

Example Question #1 : Modeling Rates Of Change, Including Related Rates Problems­

Example Question #2 : Modeling Rates Of Change, Including Related Rates Problems­

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Example Question #1 : Modeling Rates Of Change, Including Related Rates Problems

Example Question #2 : Modeling Rates Of Change, Including Related Rates Problems