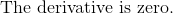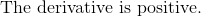Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=-1\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is negative.}$

$\text{The derivative is zero.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-1\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #42 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=7\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is negative.}$

$\text{The derivative is zero.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=7\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #43 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Conclude if the derivative of the function above at the point }\\&x=3\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=3\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #51 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Conclude if the derivative of the function above at the point }\\&x=2\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is negative.}$

$\text{The derivative is positive.}$

$\text{The derivative is zero.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=2\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #52 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Conclude if the derivative of the function above at the point }\\&x=-0.2\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is zero}$

$\text{The derivative is negative.}$

$\text{The derivative is positive.}$

Correct answer:

$\text{The derivative is zero}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-0.2\text{, the function appears to be flat.}\\&\text{The derivative is zero}\end{align*}$

Report an Error

Example Question #53 : Derivative At A Point

Functionplot

$\begin{align*}&\text{Determine whether or not the derivative of the function above at the point }\\&x=-0.8\\&\text{is positive, negative, or zero.}\end{align*}$

Possible Answers:

$\text{The derivative is positive.}$

$\text{The derivative is zero.}$

$\text{The derivative is negative.}$

Correct answer:

$\text{The derivative is positive.}$

Explanation:

$\begin{align*}&\text{The derivative of a function at a given point is synonymous}\\&\text{with the slope of a function at a given point. Therefore if}\\&\text{the function increases in value as x increases across a point,}\\&\text{the slope and derivative are positive. Conversely, if the function}\\&\text{decreases in value as x increases across a point, both slope}\\&\text{and derivative are negative. At points where the function is}\\&\text{flat, the slope and derivative are zero.}\\&\text{Studying the slope at }x=-0.8\text{, the function appears to be increasing.}\\&\text{The derivative is positive.}\end{align*}$

Report an Error

Example Question #54 : Derivative At A Point

Find the slope of the tangent line to the following function at x=3:

f(x)=10x^3+1

Possible Answers:

181

180

271

270

Correct answer:

270

Explanation:

The slope of the tangent line to a curve is given by the first derivative evaluated at the point of interest.

The first derivative of the function is equal to

f'(x)=30x^2

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

To find the slope of the tangent line at x=3, we simply evaluate the first derivative function at x=3:

f'(3)=30(3^2)=270

Report an Error

Example Question #151 : Ap Calculus Ab

Find the slope of the curve y=3x^5+9x+3 at the point x=1

Possible Answers:

Correct answer:

Explanation:

To find the slope of the curve at any point, we take its derivative

y'=15x^4+9

We then evaluate ate the point x=1 ,

y'(1)=15(1)^4+9=24

Report an Error

Example Question #152 : Ap Calculus Ab

Find k'(1) if $k(x)=\frac{3x^2+4x-2}{10}$ .

Possible Answers:

Correct answer:

Explanation:

First, find the derivative. You should get $k'(x)=\frac{1}{10}(6x+4)$ .

Next, plug in x=1.

You should get k'(1)=1 .

Report an Error

Example Question #153 : Ap Calculus Ab

Find the slope of the curve at the specified point:

y=2x^3+4x-10 at the point x=1

Possible Answers:

Correct answer:

Explanation:

To find the slope of the curve, we take the derivative of the function:

$y'=m=\frac{\mathrm{d} }{\mathrm{d} x}(2x^3+4x-10)=6x^2+4$

Evaluating the slope at the specified point, we get

y'(1)=6(1^2)+4=10

Report an Error

View AP Calculus AB Tutors

Ying
Certified Tutor

Iowa State University, Master of Science, Mathematics.

View AP Calculus AB Tutors

Bertha
Certified Tutor

California Institute of Technology, Bachelor's (in progress), Chemical Engineering.

View AP Calculus AB Tutors

Lauren
Certified Tutor

Christopher Newport University, Bachelor of Science, Neuroscience. Christopher Newport University, Bachelor of Science, Psych...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Dallas Fort Worth, English Tutors in New York City, Computer Science Tutors in New York City, Statistics Tutors in San Francisco-Bay Area, French Tutors in San Diego, Chemistry Tutors in Philadelphia, Statistics Tutors in Miami, ISEE Tutors in Washington DC, LSAT Tutors in Seattle, Math Tutors in Seattle

Popular Courses & Classes

ACT Courses & Classes in Los Angeles, SAT Courses & Classes in Seattle, ACT Courses & Classes in Washington DC, GRE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Miami, SSAT Courses & Classes in Houston, ACT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Phoenix, SAT Courses & Classes in Denver, GRE Courses & Classes in Phoenix

Popular Test Prep

GRE Test Prep in Atlanta, ACT Test Prep in Los Angeles, ACT Test Prep in Washington DC, SSAT Test Prep in Boston, SAT Test Prep in Houston, GRE Test Prep in Miami, ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Washington DC, SSAT Test Prep in Atlanta, SSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #41 : Derivative At A Point

Example Question #42 : Derivative At A Point

Example Question #43 : Derivative At A Point

Example Question #51 : Derivative At A Point

Example Question #52 : Derivative At A Point

Example Question #53 : Derivative At A Point

Example Question #54 : Derivative At A Point

Example Question #151 : Ap Calculus Ab

Example Question #152 : Ap Calculus Ab

Example Question #153 : Ap Calculus Ab

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: