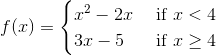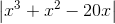is not differentiable at  and  because the values are discontinuities.  is not differentiable at  because that point is a corner, indicating that the one-side limits at  are different.  is differentiable:the one side limits are the same and the point is continuous. 

Note that , indicating that there is a horizontal tangent on  at . More specifically, the derivative is the slope of the tangent line. If the slope of the tangent line is 0, then the tangent is horizontal.

The other two are incorrect because sharp turns only apply when we want to take the derivative of something. The derivative of a function at a sharp turn is undefined, meaning the graph of the derivative will be discontinuous at the sharp turn. (To see why, ask yourself if the slope at  is positive 1 or negative 1?) On the other hand, integration is less picky than differentiation: We do not need a smooth function to take an integral.

In this case, to get from  to , we took an integral, so it didn't matter that there was a sharp turn at the specified point. Thus, neither function had any discontinuities. 

Even though an antideritvative of  does not exist, we can still use the Fundamental Theorem of Calculus to "cancel out" the integral sign in this expression.

. Start

. You can "cancel out" the integral sign with the derivative by making sure the lower bound of the integral is a constant, the upper bound is a differentiable function of , , and then substituting  in the integrand. Lastly the Theorem states you must multiply your result by  (similar to the directions in using the chain rule).

.

The function  represents the area under the curve  from  to some value of .  

Do not be confused by the use of  in the integrand. The reason we use  is because are writing the area as a function of , which requires that we treat the upper limit of integration as a variable . So we replace the independent variable of  with a dummy index  when we write down the integral. It does not change the fundamental behavior of the function  or . 

  The graph of the derivative of  is the same as the graph for . This follows directly from the Second Fundamental Theorem of Calculus.

If the function  is continuous on an interval  containing , then the function defined by: 

has for its' derivative . 

Here we could use the Fundamental Theorem of Calculus to evaluate the definite integral; however, that might be difficult and messy.

Instead, we make a clever observation of the graph of

Namely, that

This means that the values of the graph when comparing x and -x are equal but opposite. Then we can conclude that

1) If a function is differentiable, then by definition of differentiability the limit defined by, 

exists. Therefore (1) is required by definition of differentiability. _______________________________________________________________

2) If a function is differentiable at a point then it must also be continuous at that point. (This is not conversely true).

For a function to be continuous at a point  we must have: 

Therefore (2) and (4) are required. 

-----------------------------------------------------------------------------------------

3) 

This is not required, the left side of the equation is the definition of a derivative at a point  for a function . The derivative at a point does not have to equal to the function value  at that point, it is equal to the slope  at that point. Therefore 3 does not have to be true. 

However, we can note that it is possible for a function and its' derivative to be equal for a given point. Sine and cosine, for instance will intersect periodically. Another example would be the exponential function  which has itself as its' derivative . 

 ______________________________________________________________

 4) See 2

_______________________________________________________________ 

5) 

Again, the function does not have to approach the same limit as its' derivative. It is possible for a function to behave in this manner, such as in the case of sine and its' derivative cosine, which will both have the same limit at points where they intersect.  

By definition of differentiability,  when the limit exists. When  exists, we say the function is 'differentiable at '.

All of the functions are differentiable at . If you examine the graph of each of the functions, they are all defined at , and do not have a corner, cusp, or a jump there; they are all smooth and connected (Not necessarily everywhere, just at ). Additionally it is not possible to have a function that is differentiable at a point, but not continuous at that same point; differentiablity implies continuity.

To answer the question, we must find an equation which satisfies two criteria:

(1) it must have limits on either side of  that approach the same value and (2) it must have a hole at .

Each of the possible answers provide situations which demonstrate each combination of (1) and (2). That is to say, some of the equations include both a limit and a y-value at , neither, or,in the case of the piecewise function, a y-value and a limit that does not exist. 

In the function, , the numerator factors to  

while the denominator factors to . As a result, the graph of this

function resembles that for , but with a hole at . Therefore, the limit

at  exists, even though the y-value is undefined at .

To find the slope at a point, we take the derivative of , substitute in , and simplify.

.

.