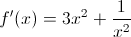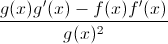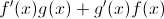Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #53 : Derivatives

What is the second derivative of 12x^2+13x+4 ?

Possible Answers:

24 x

24x+13

144

Correct answer:

Explanation:

To find the second derivative, first we need to find the first derivative.

To do that, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.

We're going to treat as 4x^0 since anything to the zero power is one.

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})+(0*4x^{0-1})$

Notice that $(0*4x^{0-1})=0$ since anything times zero is zero.

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})$

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{1})+(1*13x^{0})$

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x^{1})+(13x^{0})$

Just like it was mentioned earlier, anything to the zero power is one.

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(24x)+(13*1)$

$\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=24x+13$

Now we repeat the process using 24x+13 as our expression.

$\frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(1*24x^{1-1})+(0*13x^{0-1})$

Like before, anything times zero is zero.

$\frac{\mathrm{d} }{\mathrm{d} x}(24x+10)=(1*24x^{1-1})$

$\frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24x^{0})$

Anything to the zero power is one.

$\frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=(24*1)$

$\frac{\mathrm{d} }{\mathrm{d} x}(24x+13)=24$

Report an Error

Example Question #301 : Computation Of The Derivative

Define $g(x) = 7x^{5} - 6x^{3} - 17x$ .

What is g ''(x) ?

Possible Answers:

$g'' (x) = 70x^{3} - 36x$

$g'' (x) = 140x^{3} - 36x -17$

$g'' (x) = 70x^{3} - 18x$

$g'' (x) = 140x^{3} - 36x$

$g'' (x) = 140x^{3} - 18x$

Correct answer:

$g'' (x) = 140x^{3} - 36x$

Explanation:

Take the derivative of , then take the derivative of .

$g(x) = 7x^{5} - 6x^{3} - 17x$

$g' (x) = 5\cdot 7x^{5-1} - 3\cdot 6x^{3-1} - 17$

$g' (x) = 35x^{4} - 18x^{2} - 17$

$g'' (x) = 4\cdot 35x^{4-1} - 2\cdot 18x^{2-1} - 0$

$g'' (x) = 140x^{3} - 36x$

Report an Error

Example Question #1 : Finding Derivative At A Point

Find $f^{'}(2)$ if the function f(x) is given by

f(x) = ln(x)

Possible Answers:

$\frac{1}{2}$

$\frac{3}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

To find the derivative at x=2 , we first take the derivative of f(x) . By the derivative rule for logarithms,

$f'(x) = \frac{1}{x}$

Plugging in x=2 , we get

$f'(2) = \frac{1}{2}$

Report an Error

Example Question #1 : Finding Derivatives

Find the derivative of the following function at the point x=3 .

f(x) = 4x^3+x+3

Possible Answers:

109

110

108

107

106

Correct answer:

109

Explanation:

Use the power rule on each term of the polynomial to get the derivative,

f'(x) = (3)(4)x^2+1

Now we plug in x=3

f'(3) = (12)(3)^2 + 1 = 109

Report an Error

Example Question #2 : Finding Derivatives

Let $f(x)=x^2\sin(x^2)$ . What is $f'\left (\frac{\sqrt{\pi}}{2} \right )$ ?

Possible Answers:

$\frac{\sqrt{2\pi}(\pi + \sqrt{2})}{4}$

$\frac{\sqrt{2\pi}(\pi + 4)}{8}$

$\frac{{2\pi}(\sqrt{\pi} + 2)}{4}$

$\frac{\sqrt{2\pi}(\pi + 2)}{4}$

$\frac{(\pi + \sqrt{2})}{8}$

Correct answer:

$\frac{\sqrt{2\pi}(\pi + 4)}{8}$

Explanation:

We need to find the first derivative of f(x). This will require us to apply both the Product and Chain Rules. When we apply the Product Rule, we obtain:

$f'(x)=\sin(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]+x^2\cdot\frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]$

In order to find the derivative of $\sin(x^2)$ , we will need to employ the Chain Rule.

$\frac{\mathrm{d} }{\mathrm{d} x}[\sin(x^2)]=\cos(x^2)\cdot\frac{\mathrm{d} }{\mathrm{d} x}[x^2]=\cos(x^2)\cdot2x$

$f'(x)=\sin(x^2)\cdot2x + x^2\cdot\cos(x^2)\cdot2x$

We can factor out a 2x to make this a little nicer to look at.

$f'(x)=2x(\sin(x^2)+x^2\cos(x^2))$

Now we must evaluate the derivative when x = $\frac{\sqrt{\pi}}{2}$ .

$f'\left (\frac{\sqrt{\pi}}{2} \right )=2\cdot\frac{\sqrt{\pi}}{2}(\sin\frac{\pi}{4}+\frac{\pi}{4}\cos\frac{\pi}{4})$

$=\sqrt{\pi}(\frac{\sqrt{2}}{2}+\frac{\pi\sqrt{2}}{8})=\sqrt{2\pi}(\frac{1}{2}+\frac{\pi}{8})=\frac{\sqrt{2\pi}(\pi + 4)}{8}$

The answer is $\frac{\sqrt{2\pi}(\pi + 4)}{8}$ .

Report an Error

Example Question #1 : Understanding Derivatives Of Sums, Quotients, And Products

Find the derivative of the following function:

$f(x) = x^3 + \frac{1}{x}$

Possible Answers:

$f'(x) = 3x^2-\frac{1}{x^2}$

f'(x) = 3x^2

f'(x) = 3x^2+x

$f'(x) = 3x^2+\frac{1}{x^2}$

$f'(x) = 3x^2-\frac{1}{x}$

Correct answer:

$f'(x) = 3x^2-\frac{1}{x^2}$

Explanation:

Since this function is a polynomial, we take the derivative of each term separately.

From the power rule, the derivative of

x^3

is simply

3x^2

We can rewrite $\frac{1}{x}$ as

$x^{-1}$

and using the power rule again, we get a derivative of

$-x^{-2}$ or $-\frac{1}{x^2}$

So the answer is

$f'(x) = 3x^2-\frac{1}{x^2}$

Report an Error

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

What is $\frac{\mathrm{d} }{\mathrm{d} x}f(x)*g(x)\mathrm{d x} ?$

Possible Answers:

f(x)g'(x)+f'(x)g(x)

f(x)*f'(x)+g(x)*g'(x)

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

f(x)g(x)+f'(x)g'(x)

f(x)g'(x)-f'(x)g(x)

Correct answer:

f(x)g'(x)+f'(x)g(x)

Explanation:

The chain rule is "first times the derivative of the second plus second times derivative of the first".

In this case, that means $\frac{\mathrm{d} }{\mathrm{d} x}f(x)*g(x)\mathrm{d x} =f(x)g'(x)+f'(x)g(x)$ .

Report an Error

Example Question #3 : Understanding Derivatives Of Sums, Quotients, And Products

Which of the following best represents $\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}$ ?

Possible Answers:

$\frac{f'(x)}{g'(x)}$

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

$\frac{g(x)g'(x)-f(x)f'(x)}{g(x)^2}$

f'(x)g(x)+g'(x)f(x)

$\frac{f(x)g'(x)-g(x)f'(x)}{g(x)^2}$

Correct answer:

$\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$

Explanation:

The question is just asking for the Quotient Rule formula.

Recall the Quotient Rule is the bottom function times the derivative of the top minus the top function times the derivative of the bottom all divided by the bottom function squared.

Given,

$\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}$

the bottom function is g(x) and the top function is f(x) . This makes the bottom derivative g'(x) and the top derivative f'(x) .

Substituting these into the Quotient Rule formula resulting in the following.

$\frac{\mathrm{d} }{\mathrm{d} x}\frac{f(x)}{g(x)}=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{(g(x))^2}$

Report an Error

Example Question #1 : Understanding Derivatives Of Exponents

Find the derivative $y^{'}$ for $y = x^{2}2^x$

Possible Answers:

$2x2^{x}-x^22^{x-1}$

$2x2^{x}+x^{3}2^{x-1}$

$2x\ln(2)2^{x}$

$x2^{x+1}+\ln(2)x^{2}2^{x}$

Correct answer:

$x2^{x+1}+\ln(2)x^{2}2^{x}$

Explanation:

The derivative must be computed using the product rule. Because the derivative of x^2 brings a down as a coefficient, it can be combined with 2^x to give $2^{x+1}$

Report an Error

Example Question #3 : Understanding Derivatives Of Exponents

$f(x) = 5 ^{x + 1}$

What is f'(x) ?

Possible Answers:

$f'(x) = \ln 5 \cdot 5 ^{x+1}$

$f'(x) = \frac{5 ^{x}}{\ln 5}$

$f'(x) = \ln 5 \cdot 5 ^{x}$

$f'(x) = \frac{5 ^{x+1}}{\ln 5}$

$f'(x) = 5 ^{x}$

Correct answer:

$f'(x) = \ln 5 \cdot 5 ^{x+1}$

Explanation:

$f(x) = 5 ^{x + 1} = 5 ^{1} \cdot 5 ^{x } = 5 \cdot 5 ^{x }$

Therefore,

$f'(x) = 5 \cdot \frac{\mathrm{d} }{\mathrm{d} x} \left ( 5 ^{x } \right )$

$\frac{\mathrm{d}}{\mathrm{d} x} \left ( a ^{x } \right ) = \ln a \cdot a ^{x }$ for any real , so $\frac{\mathrm{d} }{\mathrm{d} x} \left ( 5 ^{x } \right ) = \ln 5 \cdot 5 ^{x}$ , and

$f'(x) = 5 \ln 5 \cdot 5 ^{x} = \ln 5 \cdot 5 \cdot 5 ^{x} = \ln 5 \cdot 5 ^{x+1}$

Report an Error

View AP Calculus AB Tutors

Mohammed
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Electrical Engineering. University of Maryland-College Park, Master...

View AP Calculus AB Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View AP Calculus AB Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Washington DC, SSAT Tutors in Atlanta, GRE Tutors in San Diego, Computer Science Tutors in Philadelphia, ACT Tutors in Miami, Statistics Tutors in Atlanta, Chemistry Tutors in Phoenix, Physics Tutors in Seattle, French Tutors in Houston, MCAT Tutors in Boston

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, ACT Courses & Classes in Atlanta, Spanish Courses & Classes in Houston, MCAT Courses & Classes in Boston, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Miami, GMAT Courses & Classes in Seattle, ACT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Boston, SAT Test Prep in San Diego, MCAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Miami, LSAT Test Prep in Los Angeles, MCAT Test Prep in Los Angeles, GRE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Dallas Fort Worth, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #53 : Derivatives

Example Question #301 : Computation Of The Derivative

Example Question #1 : Finding Derivative At A Point

Example Question #1 : Finding Derivatives

Example Question #2 : Finding Derivatives

Example Question #1 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #2 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #3 : Understanding Derivatives Of Sums, Quotients, And Products

Example Question #1 : Understanding Derivatives Of Exponents

Example Question #3 : Understanding Derivatives Of Exponents

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: