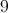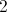Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Solving Equations

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Solving Equations

Solve f(-14) if $f(x)=-0.5x+\frac{42}{x}$ .

Possible Answers:

Correct answer:

Explanation:

Plug in for in the f(x) equation to get

$f(-14)=7+(\frac{42}{-14})=7-3=4$

Report an Error

Example Question #3369 : Algebra 1

Solve for f(x) . When x=2 .

f(x)=5x^3+2x-24

Possible Answers:

f(x)=10

f(x)=-20

f(x)=20

f(x)=14

f(x)=-15

Correct answer:

f(x)=20

Explanation:

Given the equation,

f(x)=5x^3+2x-24 and x=2

Plug in for to the equation, f(2)=5(2)^3+2(2)-24

Solve and simplify.

f(2)=5(8)+4-24

f(2)=40+4-24

f(2)=44-24

f(2)=20

Report an Error

Example Question #3371 : Algebra 1

$f(x)=\frac{4x-2}{x+3}, x\neq-3$

Solve for f(x) , when x=0 .

Possible Answers:

$f(x)=\frac{-2}{3}$

$f(x)=\frac{-1}{3}$

$f(x)=\frac{2}{3}$

$f(x)=\frac{1}{3}$

f(x)=0

Correct answer:

$f(x)=\frac{-2}{3}$

Explanation:

$f(x)=\frac{4x-2}{x+3}, x\neq-3$

Plug in the value for .

$f(0)=\frac{4(0)-2}{(0)+3}$

Simplify

$f(0)=\frac{0-2}{3}$

Subtract

$f(0)=\frac{-2}{3}$

Report an Error

Example Question #1 : Systems Of Equations

x+y=32

and

$x=\frac{2}{3}y-2$

Solve for and .

Possible Answers:

$y=19\frac{2}{5},x=12\frac{3}{5}$

$y=20\frac{3}{5},x=11\frac{4}{5}$

$y=11\frac{2}{5},x=20\frac{3}{5}$

$y=20\frac{2}{5},x=11\frac{3}{5}$

None of the available answers

Correct answer:

$y=20\frac{2}{5},x=11\frac{3}{5}$

Explanation:

x+y=32 rearranges to

x=32-y

and

$x=\frac{2}{3}y-2$ , so

$32-y=\frac{2}{3}y-2$

$32-1\frac{2}{3}y=-2$

$-1\frac{2}{3}y=-34$

$-\frac{5}{3}y=-34$

$y=\frac{-34}{1}\cdot\frac{-3}{5}=\frac{102}{5}=20\frac{2}{5}$

$x=32-20\frac{2}{5}=11\frac{3}{5}$

Report an Error

Example Question #8 : Systems Of Equations

Solve for (x, y) in the system of equations:

y = 3x + 4

2x + 3y = 34

Possible Answers:

(5, 19)

(4, 16)

The system has no solution

(3, 13)

(2, 10)

Correct answer:

(2, 10)

Explanation:

In the second equation, you can substitute 3x + 4 for from the first.

2x + 3y = 34

2x + 3 (3x + 4) = 34

2x + 3 (3x) + 3 (4) = 34

2x + 9x + 12 = 34

11x + 12 = 34

11x = 22

x = 2

Now, substitute 2 for in the first equation:

y = 3x + 4

y = 3 (2) + 4

y = 6 + 4

y = 10

The solution is (2, 10)

Report an Error

Example Question #23 : How To Find The Solution To An Equation

Solve for :

ax-b=cd

Possible Answers:

$\frac{a}{cd+b}$

$\frac{cd+a}{b}$

$\frac{b}{cd+a}$

$\frac{cd+b}{a}$

None of the other answers

Correct answer:

$\frac{cd+b}{a}$

Explanation:

To solve for , you must isolate it from the other variables. Start by adding to both sides to give you ax=cd+b . Now, you need only to divide from both sides to completely isolate . This gives you a solution of $x=\frac{cd+b}{a}$ .

Report an Error

Example Question #81 : Functions And Lines

For the following equation, if x = 2, what is y?

y=x^3-4x+9

Possible Answers:

Correct answer:

Explanation:

On the equation, replace x with 2 and then simplify.

y=x^3-4x+9

y=(2)^3-4(2)+9

y=8-8+9

y=9

Report an Error

Example Question #5 : How To Factor An Equation

Solve for $\small x$ .

x^2-5x-36

Possible Answers:

$x=-6,\ 4$

$x=-2,\ 5$

$x=-4,\ 9$

$x=2,\ 12$

$x=0,\ 3$

Correct answer:

$x=-4,\ 9$

Explanation:

x^2-5x-36

This is a quadratic equation. We can solve for $\small x$ either by factoring or using the quadratic formula. Since this equation is factorable, I will present the factoring method here.

The factored form of our equation should be in the format (A+B)(C+D)=0 .

To yield the first value in our original equation ( $\small x^2$ ), $\small A=x$ and $\small C=x$ .

(x+B)(x+D)=0

To yield the final term in our original equation ( $\small -36$ ), we can set $\small B=-9$ and $\small D=4$ .

$-9*4=-36\ \text{and}\ -9+4=-5$

(x-9)(x+4)=0

Now that the equation has been factored, we can evaluate $\small x$ . We set each factored term equal to zero and solve.

$\begin{matrix} x-9=0 &x+4=0 \\ x-9+9=0+9&x+4-4=0-4 \\ x=9 & x=-4 \end{matrix}$

Report an Error

Example Question #31 : Equations / Solution Sets

Without drawing a graph of either equation, find the point where the two lines intersect.

Line 1 : y = 3x

Line 2 : y = x - 2

Possible Answers:

(-1,-3)

(1,3)

(2,0)

(0,-2)

(0,0)

Correct answer:

(-1,-3)

Explanation:

To find the point where these two lines intersect, set the equations equal to each other, such that is substituted with the side of the second equation. Solving this new equation for will give the -coordinate of the point of intersection.

3x = x - 2

Subtract from both sides.

(3x) - x = (x - 2) - x

2x = - 2

Divide both sides by 2.

$\frac{2x}{2} = \frac{-2}{2}$

x = - 1

Now substitute into either equation to find the -coordinate of the point of intersection.

y = 3x

y= 3(-1)

y = -3

With both coordinates, we know the point of intersection is (-1,-3) . One can plug in for and for in both equations to verify that this is correct.

Report an Error

Example Question #33 : Equations / Solution Sets

What is the sum of and for the following system of equations?

3x - 5y = 5

-2x + 5y = 0

Possible Answers:

Correct answer:

Explanation:

3x - 5y = 5

-2x + 5y = 0

Add the equations together.

3x+(-2x)=x

-5y+5y=0

5+0=5

Put the terms together to see that $x+0=5\ \textup{or}\ x=5$ .

Substitute this value into one of the original equaitons and solve for .

3x - 5y = 5

3(5) - 5y = 5

-5y=-10

y=2

Now we know that $x=5\ \textup{and}\ y=2$ , thus we can find the sum of and .

x+y=5+2=7

Report an Error

View Algebra 2 Tutors

Shakeel
Certified Tutor

View Algebra 2 Tutors

Hayley
Certified Tutor

University of North Florida, Bachelor in Arts, English.

View Algebra 2 Tutors

Morgan
Certified Tutor

Catholic University of America, Bachelor of Science, International Finance.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Atlanta, ACT Tutors in Los Angeles, Chemistry Tutors in Washington DC, Statistics Tutors in Seattle, Biology Tutors in Boston, Chemistry Tutors in Phoenix, Computer Science Tutors in San Francisco-Bay Area, Statistics Tutors in Philadelphia, SAT Tutors in Washington DC, SAT Tutors in Denver

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Phoenix, Spanish Courses & Classes in Phoenix, Spanish Courses & Classes in Houston, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, LSAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, GRE Courses & Classes in Houston

Popular Test Prep

MCAT Test Prep in Dallas Fort Worth, GRE Test Prep in Seattle, GMAT Test Prep in Atlanta, SSAT Test Prep in Houston, MCAT Test Prep in Houston, SSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in New York City, MCAT Test Prep in Miami, ACT Test Prep in Atlanta, ISEE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Solving Equations

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #31 : Solving Equations

Example Question #3369 : Algebra 1

Example Question #3371 : Algebra 1

Example Question #1 : Systems Of Equations

Example Question #8 : Systems Of Equations

Example Question #23 : How To Find The Solution To An Equation

Example Question #81 : Functions And Lines

Example Question #5 : How To Factor An Equation

Example Question #31 : Equations / Solution Sets

Example Question #33 : Equations / Solution Sets

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: