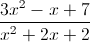In order to determine the least common denominator, we will need to multiply both denominators together.  Be careful not to mix up the denominators as similar entities.

Do not solve the problem.  

The answer is:  

The least common denominator is the term that is both divisible by all denominators and do not have common denominators smaller than this term.

Notice that both denominators can share a .  We can simply change the first denominator to  by multiplying an x-term.

For the second denominator, notice that we can change the three to a nine, similar to the first denominator by multiplying a three.

Since these terms are common and is the least possible term, this is the least common denominator.

The answer is:  

In order to determine the least common denominator, we will need to break up both denominator with their simplest forms.

Notice that both of the values share an  term.  The first expression lacks a two coefficient, and the second expression lacks an  term.

This means that the LCD will be:  

Simplify this expression by distribution.

The answer is:  

This is a more complicated form of

Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators.  Simplify as needed.

which is equivalent to

Simplify to get

Because the two rational expressions have the same denominator, we can simply add straight across the top.  The denominator stays the same.

Therefore the answer is .

a.  Find a common denominator by identifying the Least Common Multiple of both denominators.  The LCM of 3 and 1 is 3.  The LCM of  and  is . Therefore, the common denominator is .

b. Write an equivialent fraction to  using  as the denominator.  Multiply both the numerator and the denominator by  to get . Notice that the second fraction in the original expression already has  as a denominator, so it does not need to be converted.

The expression should now look like: . 

c. Subtract the numerators, putting the difference over the common denominator.

To combine fractions of different denominators, we must first find a common denominator between the two. We can do this by multiplying the first fraction by  and the second fraction by . We therefore obtain:

Since these fractions have the same denominators, we can now combine them, and our final answer is therefore:

We start by adjusting both terms to the same denominator which is 2 x 3 = 6

Then we adjust the numerators by multiplying x+1 by 2 and 2x-5 by 3

The results are:

So the final answer is,

Start by putting both equations at the same denominator. 

2x+4 = (x+2) x 2 so we only need to adjust the first term: 

Then we subtract the numerators, remembering to distribute the negative sign to all terms of the second fraction's numerator:

(x+5)(x+3) is the common denominator for this problem making the numerators 7(x+3) and 8(x+5).

7(x+3)+8(x+5)= 7x+21+8x+40= 15x+61

A=61