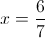All Algebra II Resources
Example Questions
Example Question #1 : Solving Non Quadratic Polynomials
Simplify:
Use the difference of squares to factor out the numerator.
The term 

Replace the fraction.
Simplify the top and bottom.
The answer is:
Example Question #2 : How To Find The Degree Of A Polynomial
What is the degree of the polynomial?
The degree is the highest exponent value of the variables in the polynomial.
Here, the highest exponent is x5, so the degree is 5.
Example Question #281 : Algebra Ii
Consider the equation 
According to the Rational Zeroes Theorem, if 
By the Rational Zeroes Theorem, any rational solution must be a factor of the constant, 6, divided by the factor of the leading coefficient, 14.
Four of the answer choices have this characteristic:

Example Question #5201 : Algebra Ii
Create a cubic function that has roots at 

This can be written as:

Multiply the terms together:
Multiply the first two terms:
FOIL:
Combine like terms:
Example Question #2 : Write A Polynomial Function From Its Zeros
Write a function in standard form with zeroes at -1, 2, and i.
from the zeroes given and the Fundamental Theorem of Algebra we know:
use FOIL method to obtain:
Distribute:
Simplify:
Example Question #1 : Write A Polynomial Function From Its Zeros
Find a polynomial function 
Find a polynomial function 
Recall that by roots of a polynomial we are referring to values of 

Because one of the roots given is a complex number, we know there must be a second root that is the complex conjugate of the given root. This is 
Because 

The other roots are complex numbers, so there must be a quadratic factor.
To find the quadratic factor start with the 
Isolate the imaginary term 
Expand the left side, and note on the right side the 
So now we have,
The quadratic factor for 


Now we carry out the multiplication to write the final form of 
Example Question #1 : Write A Polynomial Function From Its Zeros
Which of the following equations represents a quadratic with zeros at 


When you're writing a quadratic having been given its zeros, the best place to start is by setting aside the coefficient and first putting together a simple, factored quadratic that would satisfy those zeros. Here with zeros at 7 and -3, that would be:
If you then expand that quadratic, you have:
Of course, that's just one possible quadratic that satisfies those zeros, and your job is to find THE quadratic that satisfies those zeroes AND passes through (0, -63). And clearly here if you plug in 


And then plugging in 

So
Meaning that 
Example Question #713 : Intermediate Single Variable Algebra
A quadratic function takes the form 

Get everyone on one side of the equation:

These are the factors of the equation. Put them together, and then multiply them to get:
Therefore, the solution to this question is
Example Question #1 : Write A Polynomial Function From Its Zeros
Which of the following equations represents a quadratic equations with zeros at 


When finding the equation of a quadratic from its zeros, the natural first step is to recreate the factored form of a simple quadratic with those zeros. Putting aside the coefficient, a quadratic with zeros at 3 and -6 would factor to:
So you know that a possible quadratic for these zeros would be:
Now you need to determine the coefficient of the quadratic, and that’s where the point (2, -24) comes in. That means that if you plug in 




This means that:
So:
And therefore 

So:
Example Question #7 : Write A Polynomial Function From Its Zeros
Which of the following represents a quadratic equation with its zeros at 

The important first step of creating a quadratic equation from its zeros is knowing what a zero really is. A zero of a quadratic (or polynomial) is an x-coordinate at which the y-coordinate is equal to 0.
We find that algebraically by factoring quadratics into the form 



Here the question gives you a head start: we know that the numbers 4 and 5 can go in the 

This satisfies the requirements of zeros, but now we need to expand this equation using FOIL to turn it into a proper quadratic. That means that our quadratic is:
And when we combine like terms it's:
Certified Tutor
Certified Tutor
All Algebra II Resources