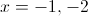First, set the inequality to zero and solve for .

Now, plot these two numbers on to a number line.

Notice how these numbers divide the number line into three regions:

Now, you will choose a number from each of these regions to test to plug back into the inequality to see if the inequality holds true.

For , let 

Since this is not less than zero, the solution to the inequality cannot be found in this region.

For , let 

Since this is less than zero, the solution is found in this region.

For , let 

Since this is not less than zero, the solution is not found in this region.

Then, the solution for this inequality is 

Start by changing the less than sign to an equal sign and solve for .

Now, plot these two numbers on a number line.

Notice how the number line is divided into three regions:

Now, choose a number fromeach of these regions to plug back into the inequality to test if the inequality holds.

For , let 

Since this number is not less than zero, the solution cannot be found in this region.

For , let 

Since this number is less than zero, the solution can be found in this region.

For  let .

Since this number is not less than zero, the solution cannot be found in this region.

Because the solution is only negative in the interval , that must be the solution.

First, set the inequality to zero and solve for .

Now, plot these two numbers on to a number line.

Notice how these numbers divide the number line into three regions:

Now, you will choose a number from each of these regions to test to plug back into the inequality to see if the inequality holds true.

For , let 

Since this solution is greater than or equal to , the solution can be found in this region.

For , let 

Since this is less than or equal to , the solution cannot be found in this region.

For , let 

Since this is greater than or equal to , the solution can be found in this region.

Because the solution can be found in every single region, the answer to this inequality is 

First, we can factor the quadratic to give us a better understanding of its graph. Factoring gives us: . Now we know that the quadratic has zeros at  and . Furthermore this information reveals that the quadratic is positive. Using this information, we can sketch a graph like this: 

We can see that the parabola is below the x-axis (in other words, less than ) between these two zeros  and .

The only x-value satisfying the inequality  is .

The value of  would work if the inequality were inclusive, but since it is strictly less than instead of less than or equal to , that value will not work.

We know that is equivalent to or .

By this property, there is no way to get from .

Therefore the correct answer is .

Because the denominator cannot be zero, the domain is all other numbers except for 1, or

This problem is a lot simpler if we factor all the expressions involved before proceeding:

Next let's remember how we divide one fraction by another—by multiplying by the reciprocal:

In this form, we can see that a lot of terms are going to start canceling with each other. All that we're left with is just .

The rational expression is a ratio of two polynomials.  

The denominator cannot be zero.

An example of a rational expression is:

The answer is:  

If or , the denominator is 0, which makes the expression undefined.

 This happens when x = 1 or when x = -2.

Therefore the correct answer is .

In order to simplify the expression , we need to ensure that both terms have the same denominator. In order to do so, find the Least Common Denominator (LCD) for both terms and simplify the expression accordingly: