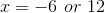To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

 and 

We can then solve these two equations to obtain

This equation describes a circle of radius  (square root of ), centered at the point .  The equation (which is NOT a function) has a maximum y-coordinate value directly above the center of the circle in the vertical direction.  Take the y-coordinate of the center, , and add to it the length of the radius, , to get the answer, .

Let

Therefore the equation becomes,

Solve for x.

Let

Therefore, the equation becomes:

Solve for y.

The equation for a circle centered at the point (h, k) with radius r units is

.

Setting , , and  yields

.

To convert degrees to radians, multiply degrees by:

Therefore 

Coterminal angles are angles that are the same but written differently. Circles have 360 degrees, so an angle that goes above this threshold has completed one revolution. For example, a 450 degree angle would be in the same position as a 90 degree angle. 

To find a positive coterminal angle, add 360 degrees to the initial value. 

To find the negative coterminal angle, simply subtract 360. The only exception to this rule would be if the initial value were greater than 360. In this case, subtract 360 until the value is negative, making it a negative coterminal. Therefore, 

160-360 = -200

Do this a second time and we get -560. These are examples of negative coterminal angles. 

The circle is represented by the formula:

Although some of the equations might not in this form, we can see by the variables that the equation   is most similar to the form.

Multiply two on both sides of the equation and we will have: 

This is an equation of a circle.  The other equations represent other conic shapes.

The answer is:  

Definition of the formula of a circle:

Where:

is the coordinate of the center of the circle

is the  coordinate of the center of the circle

is the radius of the circle

Plugging in values:

In order to solve for the radius, we will need to complete the square twice.  

Group the x and y-variables in parentheses.  Starting from the original equation:

Add two on both sides. 

Divide by the second term coefficient of each binomial by 2, and add the squared quantity on both sides of the equation.

The equation becomes:

Factorize both polynomials in parentheses and simplify the right side.

The center is: 

The radius is:  

The answer is: