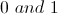To solve this problem, we could complete the square and shift the equation that way, but the vertex ends up being  so this may not be an ideal method. Instead, we know we're shifting the equation 3 units to the right, so we can just plug in for every appearance of x:

To simplify, first expand

Now we can plug that in and continue simplifying:

distribute the 2; combine -3 and -5

combine like terms -12x and x; 18 and -8

Now we want to flip this over the x-axis, meaning that the y coordinates change sign.

This means we have to multiply everything by -1, or simply change the sign of every term on the right side:

Below is the standard equation for parabolas;

Therefore,

 and 

thus,

the translation from the parent function is down three units, right one unit.

Shifting up and down will result in a change in the y-intercept.

Add four to the equation.

Shifting the parabola to the left two units will change the inner term  to , which will be .

Replace the  quantity with .

The new equation is:  

Vertical shifts will change the value of the y-intercept.  Since this function is to be shifted up two units, add two to the right side of the equation.

This graph shifted two units to the left indicates that its zeros will also shift to the left two units, which means that the  term will become .

Rewrite the equation and expand the binomials.

The new equation is:  

Shifting this graph three units to the right means that the x-variable will need to be replaced with .  Rewrite the equation.

Use the FOIL method to simplify the binomial.

Simplify the right side.

The equation becomes:  

The answer is:  

To determine how "wide" or "skinny" a parabola is, we look at the leading coefficient. 

The smaller the fraction, the wider a parabola will be. 

The larger the whole number, the skinnier the parabola will be. 

This will give us the widest parabola. 

Simplify the following equation by using the FOIL method with the binomial.

Simplify all terms in the parentheses.

Replace the term and simplify.

The equation in standard form is:  

Since this parabola is shifted up one unit, add one to the y-intercept.

The answer is:  

First, reflect the equation over the y-axis by switching the sign of x:

Now shift up 2 by adding 2:

Now shift left 4 by adding 4 to x:

 first expand

Now multiply

Now plug those back in:

combine like terms

To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

 and 

We can then solve these two equations to obtain .