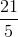Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Irrational Numbers

Which of the following is an irrational number?

Possible Answers:

5.75

$\pi$

$\sqrt{9}$

$0.\overline{3333}$

$\frac{21}{5}$

Correct answer:

$\pi$

Explanation:

A rational number can be expressed as a fraction of integers, while an irrational number cannot.

$0.\overline{3333}$ can be written as $\frac{1}{3}$ .

$\sqrt{9}$ is simply , which is a rational number.

The number 5.75 can be rewritten as a fraction of whole numbers, $\frac{23}{4}$ , which makes it a rational number.

$\frac{21}{5}$ is also a rational number because it is a ratio of whole numbers.

The number, $\pi$ , on the other hand, is irrational, since it has an irregular sequence of numbers ( 3.14159 ...) that cannot be written as a fraction.

Report an Error

Example Question #1 : Number Sets

If $A= \left \{ 10, 20, 30, 40, 50 \right \}$ , $B=\left \{ 10, 20, 40, 60 \right \}$ , and $C=\left \{ 20, 30, 40, 60 \right \}$ , then find the following set:

$A\cup B$

Possible Answers:

$\left \{ 10, 20, 40, 60 \right \}$

$\left \{ 10, 20, 40, 50, 60 \right \}$

$\left \{ 10, 20, 40 \right \}$

$\left \{ 10, 20, 30, 40, 50 \right \}$

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

Correct answer:

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

Explanation:

The union is the set that contains all the numbers from $A= \left \{ 10, 20, 30, 40, 50 \right \}$ and $B=\left \{ 10, 20, 40, 60 \right \}$ . Therefore the union is $\left \{ 10, 20, 30, 40, 50, 60 \right \}$ .

Report an Error

Example Question #71 : Number Theory

If $A= \left \{ 10, 20, 30, 40, 50 \right \}$ , $B=\left \{ 10, 20, 40, 60 \right \}$ , and $C=\left \{ 20, 30, 40, 60\right \}$ , find the following set:

$A\cap B\cap C$

Possible Answers:

$\left \{ 20, 40, 60 \right \}$

$\left \{ 20, 40 \right \}$

$\left \{ 20, 30, 40 \right \}$

$\left \{ 40 \right \}$

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

Correct answer:

$\left \{ 20, 40 \right \}$

Explanation:

The intersection is the set that contains only the numbers found in all three sets. Therefore the intersection is $\left \{ 20, 40 \right \}$ .

Report an Error

Example Question #2 : Number Sets

If $A= \left \{ 10, 20, 30, 40, 50 \right \}$ , $B=\left \{ 10, 20, 40, 60 \right \}$ , and $C=\left \{ 20, 30, 40, 60 \right \}$ , find the following set:

$B\cap C$

Possible Answers:

$\left \{ 40, 60 \right \}$

$\left \{10, 20, 40 \right \}$

$\left \{ 20, 40, 60 \right \}$

$\left \{ 10, 20, 40, 60 \right \}$

$\left \{ 20, 40 \right \}$

Correct answer:

$\left \{ 20, 40, 60 \right \}$

Explanation:

The intersection is the set that contains the numbers that appear in both $B=\left \{ 10, 20, 40, 60 \right \}$ and $C=\left \{ 20, 30, 40, 60 \right \}$ . Therefore the intersection is $\left \{ 20, 40, 60 \right \}$ .

Report an Error

Example Question #2 : Number Sets

If $A=\left \{ 10, 20, 30, 40, 50\right \}$ , $B=\left \{ 10, 20, 40, 60 \right \}$ , and $C=\left \{ 20, 30, 40, 60 \right \}$ , find the following set:

$A\cap C$

Possible Answers:

$\left \{ 20, 40 \right \}$

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

$\left \{ 20, 30, 40, 60 \right \}$

$\left \{ 20, 30, 40 \right \}$

$\left \{ 30, 40 \right \}$

Correct answer:

$\left \{ 20, 30, 40 \right \}$

Explanation:

The intersection is the set that contains the numbers found in both sets. Therefore the intersection is $\left \{ 20, 30, 40 \right \}$ .

Report an Error

Example Question #4 : Number Sets

If $A=\left \{ 10, 20, 30, 40, 50\right \}$ , $B=\left \{ 10, 20, 40, 60 \right \}$ , and $C=\left \{ 20, 30, 40, 60\right \}$ , find the following set:

$A\cup B\cup C$

Possible Answers:

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

$\left \{ 10, 20, 30, 40, 50 \right \}$

$\left \{ 10, 20, 40, 60 \right \}$

$\left \{ 20, 40, 60 \right \}$

$\left \{ 40, 60 \right \}$

Correct answer:

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

Explanation:

The union is the set that contains all of the numbers found in all three sets. Therefore the union is $\left \{ 10, 20, 30, 40, 50, 60 \right \}$ . You do not need to re-write the numbers that appear more than once.

Report an Error

Example Question #5 : Number Sets

If $A=\left \{ 10, 20, 30, 40, 50\right \}$ , $B=\left \{ 10, 20, 40, 60\right \}$ , and $C=\left \{ 20, 30, 40, 60\right \}$ , find the following set:

$A\cap B$

Possible Answers:

$\left \{ 20, 40 \right \}$

$\left \{ 10, 20, 40 \right \}$

$\left \{ 10, 20, 40, 60 \right \}$

$\left \{ 20, 40, 60 \right \}$

$\left \{ 10, 20, 30, 40, 50, 60 \right \}$

Correct answer:

$\left \{ 10, 20, 40 \right \}$

Explanation:

The intersection is the set that contains the numbers found in both sets. Therefore the intersection is $\left \{ 10, 20, 40 \right \}$ .

Report an Error

Example Question #1 : Number Sets

Sets3

Which set of numbers represents the union of E and F?

Possible Answers:

70,15

35,60,15,70,250

60,15,75,140,250,70

70,15,60,75

{35,70,15,60,75,250}

Correct answer:

{35,70,15,60,75,250}

Explanation:

The union is the set of numbers that lie in set E or in set F.

. Sets3

In this problem set E contains terms 35,60,15,70 , and set F contains terms 250,70,15,75 . Therefore, the union of these two sets is 35,60,15,70,75,250 .

Report an Error

Example Question #11 : How To Find The Domain Of A Function

Express the following in Set Builder Notation:

$\left ( -\infty , -3\ \right )\cup \left ( -3, 1 \right )\cup \left ( 1, \infty \right )$

Possible Answers:

$\left \{ x|-\infty < x< 1 \right \}$

$\left \{ x|-3< x< 1 \right \}$

$\left \{ x|-\infty< x< -3 \right\ OR\ -3< x< 1\ OR\ 1< x< \infty \}$

$\left \{ x|-\infty < x< -3 \right \}$

$\left \{ x|-3< x< \infty \right \}$

Correct answer:

$\left \{ x|-\infty< x< -3 \right\ OR\ -3< x< 1\ OR\ 1< x< \infty \}$

Explanation:

$\left ( -\infty , -3 \right ) = \left \{x| -\infty < x< -3 \right \}$

and $\cup$ stands for OR in Set Builder Notation

Report an Error

Example Question #1 : Number Sets

Find the intersection of the two sets:

$A=\left \{ 1, 2, 3, 4, 5, 6, 7, 8 \right \}, B=\left \{ 2, 4, 6, 7, 9 \right \}$

Possible Answers:

$\left \{ 1, 3, 5, 8, 9 \right \}$

$\left \{ 1, 2, 3, 4, 5, 6, 7, 8,9 \right \}$

$\left \{ 2, 4, 6, 7 \right \}$

$\left \{ \right \}$

Correct answer:

$\left \{ 2, 4, 6, 7 \right \}$

Explanation:

To find the intersection of the two sets, $A\cap B$ , we must find the elements that are shared by both sets:

$\left \{ 2, 4, 6, 7 \right \}$

Report an Error

View Algebra 2 Tutors

Adriana
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Mathematics. University of Connecticut, Master of Science, Mathematics.

View Algebra 2 Tutors

G Samuel
Certified Tutor

Loyola College, Madras, Bachelor in Arts, Accounting.

View Algebra 2 Tutors

Jyotiparna
Certified Tutor

Vellore Institute of Technology, Bachelor of Technology, Chemical Engineering. University of Toronto, Master of Engineering, ...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Dallas Fort Worth, Computer Science Tutors in Denver, MCAT Tutors in Boston, Reading Tutors in Atlanta, ISEE Tutors in Phoenix, Spanish Tutors in Boston, Calculus Tutors in Miami, SAT Tutors in Houston, Computer Science Tutors in Boston, Chemistry Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Denver, LSAT Courses & Classes in Atlanta, SAT Courses & Classes in Miami, ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Phoenix, SSAT Courses & Classes in New York City, SSAT Courses & Classes in Houston, LSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SSAT Test Prep in Los Angeles, ACT Test Prep in Washington DC, GRE Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, LSAT Test Prep in Houston, LSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Atlanta, ACT Test Prep in San Diego, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : Irrational Numbers

Example Question #1 : Number Sets

Example Question #71 : Number Theory

Example Question #2 : Number Sets

Example Question #2 : Number Sets

Example Question #4 : Number Sets

Example Question #5 : Number Sets

Example Question #1 : Number Sets

Example Question #11 : How To Find The Domain Of A Function

Example Question #1 : Number Sets

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: