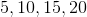The iteration starts at zero and ends at three.

Substitute the terms and increase the value of  by one for each loop.

Simplify the terms.

The answer is:  

 is equal to the sum of the expressions formed by substituting 1, 2, 3, and 4, in turn, for  in the expression , as follows:

The finite sequence can be restated, and evaluated, as

.

 is equal to the sum of the expressions formed by substituting 1, 2, 3, 4, and 5, in turn, for  in the expression , as follows: 

:

The finite series can be restated, and evaluated, as 

.

Substitute the value of  for each iteration.

Simplify each term by order of operations.

Convert all with a common denominator.

The answer is:  

An arithmetic sequence is one in which the common difference is added to one term to get the next term. Thus, if the first term is 3, we add 5 to get the second term, and continue in this manner. 

Thus, the first four terms are: 

This is an arithmetic sequence since the difference between consecutive terms is the same ().  To find the th term of an arithmetic sequence, use the formula

,

where  is the first term,  is the number of terms, and  is the difference between terms.  In this case,  is ,  is , and  is . 

The question states that the sequence is arithmetic, which means we find the next number in the sequence by adding (or subtracting) a constant term. We know two of the values, separated by one unknown value.

We know that  is equally far from -1 and from 13; therefore  is equal to half the distance between these two values. The distance between them can be found by adding the absolute values.

The constant in the sequence is 7. From there we can go forward or backward to find out that .

By taking the difference between two adjacent numbers in the sequence, we can see that the common difference increases by one each time.

Our next term will fit the equation , meaning that the next term must be .

After , the next term will be , meaning that the next term must be .

Finally, after , the next term will be , meaning that the next term must be

The question asks for the sum of the next three terms, so now we need to add them together.

In each group of numbers, compare the difference of the second and first terms to that of the third and second terms. The group in which they are unequal is the correct choice.

The last group of numbers is the correct choice.

In arithmetic sequences, the common difference is simply the value that is added to each term to produce the next term of the sequence. When solving this equation, one approach involves substituting 5 for  to find the numbers that make up this sequence. For example, 

so 14 is the first term of the sequence. However, a much easier approach involves only the last two terms,  and .

The difference between these expressions is 8, so this must be the common difference between consecutive terms in the sequence.