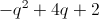Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Multiply A Monomial By A Polynomial

Expand: 8x(3x+7)

Possible Answers:

24x^2 + 56

24x^2 + 56x

24x + 56

11x + 15

11x^2 + 15x

Correct answer:

24x^2 + 56x

Explanation:

To expand, multiply 8x by both terms in the expression (3x + 7).

8x multiplied by 3x is 24x².

8x multiplied by 7 is 56x.

Therefore, 8x(3x + 7) = 24x² + 56x.

Report an Error

Example Question #1941 : Algebra Ii

Simplify:

-5(x+15)-3x

Possible Answers:

2x-75

None of the other answers are correct.

2x+15

-8x-75

-8x+15

Correct answer:

-8x-75

Explanation:

First, distribute –5 through the parentheses by multiplying both terms by –5.

-5(x+15)-3x=-5x-75-3x

Then, combine the like-termed variables (–5x and –3x).

-5x-75-3x=-8x-75

Report an Error

Example Question #1 : How To Multiply Binomials With The Distributive Property

Expand:

$\frac{1}{3}(2x^2-6)(4x-\frac{2}{3})$

Possible Answers:

$2\frac{2}{3}x^3+\frac{4}{9}x^2-8x+1\frac{1}{3}$

$2\frac{2}{3}x^3-\frac{4}{9}x^2-8x+1\frac{1}{3}$

$2\frac{2}{3}x^3-\frac{4}{9}x^2+8x+1\frac{1}{3}$

$2\frac{2}{3}x^3-\frac{4}{9}x^2-8x-1\frac{1}{3}$

$-2\frac{2}{3}x^3-\frac{4}{9}x^2-8x+1\frac{1}{3}$

Correct answer:

$2\frac{2}{3}x^3-\frac{4}{9}x^2-8x+1\frac{1}{3}$

Explanation:

First, FOIL:

$\frac{1}{3}(8x^3-\frac{4}{3}x^2-24x+\frac{12}{3})$

Simplify:

$\frac{1}{3}(8x^3-\frac{4}{3}x^2-24x+4)$

Distribute the $\frac{1}{3}$ through the parentheses:

$\frac{8}{3}x^3-\frac{4}{9}x^2-\frac{24}{3}x+\frac{4}{3}$

Rewrite to make the expression look like one of the answer choices:

$2\frac{2}{3}x^3-\frac{4}{9}x^2-8x+1\frac{1}{3}$

Report an Error

Example Question #101 : Basic Single Variable Algebra

Simplify the expression.

$15x^{3}y^{2}+8x^{2}+3x^{3}y^{2}-4x^{2}$

Possible Answers:

$22x^3y^{2}x^{2}$

$22x^{6}y^{4}$

None of the other answers are correct.

$18x^{3}y^{2}-4x^{2}$

$18x^{3}y^{2}+4x^{2}$

Correct answer:

$18x^{3}y^{2}+4x^{2}$

Explanation:

When simplifying polynomials, only combine the variables with like terms.

$15x^{3}y^{2}$ can be added to $3x^{3}y^{2}$ , giving $18x^{3}y^{2}$ .

$4x^{2}$ can be subtracted from $8x^{2}$ to give $4x^{2}$ .

Combine both of the terms into one expression to find the answer: $18x^{3}y^{2}+4x^{2}$

Report an Error

Example Question #102 : Basic Single Variable Algebra

Simplify the following expression.

$(5c^{2}+5)+(-5c-5)$

Possible Answers:

$5c^{2}-5c$

$5c^{2}-5c-25$

$5c^{2}-5c+10$

Correct answer:

$5c^{2}-5c$

Explanation:

$(5c^{2}+5)+(-5c-5)$

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms to solve.

$5c^{2}$ and -5c have no like terms and cannot be combined with anything.

5 and -5 can be combined however:

5-5=0

This leaves us with $5c^{2}-5c$ .

Report an Error

Example Question #103 : Basic Single Variable Algebra

Simplify the following:

4x^3-2x(x-2)(x+3)

Possible Answers:

4x^3-2x(x^2+x-6)

4x^3-2x^3-2x^2+12x

2x^3-2x^2+12x

8x^3-2x+16

None of the other answers are correct.

Correct answer:

2x^3-2x^2+12x

Explanation:

4x^3-2x(x-2)(x+3)

First, FOIL the two binomials:

4x^3-2x(x^2+x-6)

Then distribute the through the terms in parentheses:

4x^3-2x^3-2x^2+12x

Combine like terms:

2x^3-2x^2+12x

Report an Error

Example Question #1 : How To Subtract Polynomials

Simplify the following expression:

$(2q^{2}+4q+7)-(3q^{2}-5)$

Possible Answers:

$-q^{2}+4q+12$

-q^2+4q+2

$-5q^{2}+4q+2$

$-3q^{2}+12$

Correct answer:

$-q^{2}+4q+12$

Explanation:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms together:

$2q^{2}-3q^{2}=-1q^{2}=-q^2$

has no like terms.

7-(-5)=12

Combine these terms into one expression to find the answer:

$-q^{2}+4q+12$

Report an Error

Example Question #1 : How To Multiply Polynomials

Simplify the expression.

$x^{5}*x^{16}$

Possible Answers:

$x^{21}$

$2x^{16}$

$x^{11}$

$x^{80}$

The expression cannot be simplified further.

Correct answer:

$x^{21}$

Explanation:

When multiplying exponential components, you must add the powers of each term together.

5+16=21

$x^{5}*x^{16}=x^{21}$

Report an Error

Example Question #15 : Simplifying Expressions

$x^{5}y^{17}*x^{2}y^{2}=?$

Possible Answers:

$x^{7}y^{19}$

$x^{2}y^{8}$

None of the other answers are correct.

$x^{10}y^{34}$

$2x^{2}x^{7}y^{19}$

Correct answer:

$x^{7}y^{19}$

Explanation:

When multiplying polynomials, add the powers of each like-termed variable together.

For x: 5 + 2 = 7

For y: 17 + 2 = 19

Therefore the answer is $x^{7}y^{19}$ .

Report an Error

Example Question #105 : Basic Single Variable Algebra

Simplify the following:

$\frac{x^2-10x+25}{x^2-25}$

Possible Answers:

$\frac{x-5}{x+5}$

$\frac{(x-5)(x-5)}{(x-5)(x+5)}$

This fraction cannot be simplified.

Correct answer:

$\frac{x-5}{x+5}$

Explanation:

$\frac{x^2-10x+25}{x^2-25}$

First we will factor the numerator:

x^2-10x+25=(x-5)(x-5)

Then factor the denominator:

x^2-25=(x+5)(x-5)

We can re-write the original fraction with these factors and then cancel an (x-5) term from both parts:

$\frac{(x-5)(x-5)}{(x-5)(x+5)}=\frac{x-5}{x+5}$

Report an Error

View Algebra 2 Tutors

Ann
Certified Tutor

Wright State University-Main Campus, Bachelor of Science, Mathematics and Computer Science. Western Governors University, Mas...

View Algebra 2 Tutors

Tiffany
Certified Tutor

Eastern Washington University, Bachelor of Education, Elementary School Teaching.

View Algebra 2 Tutors

Jennifer
Certified Tutor

Baylor University, Bachelor of Science, Biochemistry. Stephen F Austin State University, Master of Science, Chemistry.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Boston, French Tutors in Phoenix, SAT Tutors in Chicago, Physics Tutors in Phoenix, Computer Science Tutors in Phoenix, Reading Tutors in Miami, Algebra Tutors in Miami, French Tutors in New York City, Algebra Tutors in San Francisco-Bay Area, MCAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

ISEE Courses & Classes in Denver, SSAT Courses & Classes in Atlanta, SAT Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Chicago, GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in New York City, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, SAT Courses & Classes in Los Angeles

Popular Test Prep

SSAT Test Prep in Denver, ACT Test Prep in Chicago, ISEE Test Prep in Los Angeles, MCAT Test Prep in Boston, SAT Test Prep in Phoenix, MCAT Test Prep in Chicago, SAT Test Prep in Boston, MCAT Test Prep in Atlanta, SAT Test Prep in Washington DC, LSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #1 : How To Multiply A Monomial By A Polynomial

Example Question #1941 : Algebra Ii

Example Question #1 : How To Multiply Binomials With The Distributive Property

Example Question #101 : Basic Single Variable Algebra

Example Question #102 : Basic Single Variable Algebra

Example Question #103 : Basic Single Variable Algebra

Example Question #1 : How To Subtract Polynomials

Example Question #1 : How To Multiply Polynomials

Example Question #15 : Simplifying Expressions

Example Question #105 : Basic Single Variable Algebra

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: