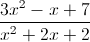This is a more complicated form of

Find the least common denominator (LCD) and convert each fraction to the LCD, then add the numerators.  Simplify as needed.

which is equivalent to

Simplify to get

Because the two rational expressions have the same denominator, we can simply add straight across the top.  The denominator stays the same.

Therefore the answer is .

a.  Find a common denominator by identifying the Least Common Multiple of both denominators.  The LCM of 3 and 1 is 3.  The LCM of  and  is . Therefore, the common denominator is .

b. Write an equivialent fraction to  using  as the denominator.  Multiply both the numerator and the denominator by  to get . Notice that the second fraction in the original expression already has  as a denominator, so it does not need to be converted.

The expression should now look like: . 

c. Subtract the numerators, putting the difference over the common denominator.

To combine fractions of different denominators, we must first find a common denominator between the two. We can do this by multiplying the first fraction by  and the second fraction by . We therefore obtain:

Since these fractions have the same denominators, we can now combine them, and our final answer is therefore:

We start by adjusting both terms to the same denominator which is 2 x 3 = 6

Then we adjust the numerators by multiplying x+1 by 2 and 2x-5 by 3

The results are:

So the final answer is,

Start by putting both equations at the same denominator. 

2x+4 = (x+2) x 2 so we only need to adjust the first term: 

Then we subtract the numerators, remembering to distribute the negative sign to all terms of the second fraction's numerator:

(x+5)(x+3) is the common denominator for this problem making the numerators 7(x+3) and 8(x+5).

7(x+3)+8(x+5)= 7x+21+8x+40= 15x+61

A=61

First factor the denominators which gives us the following:

The two rational fractions have a common denominator hence they are like "like fractions".  Hence we get:

Simplifying gives us

First let us find a common denominator as follows:

Now we can subtract the numerators which gives us :

So the final answer is

With rational equations we must first note the domain, which is all real numbers except . (Recall, the denominator cannot equal zero. Thus, to find the domain set each denominator equal to zero and solve for what the variable cannot be.) 

The least common denominator or  and  is . Multiply every term by the LCD to cancel out the denominators. The equation reduces to . We can FOIL to expand the equation to . Combine like terms and solve: . Factor the quadratic and set each factor equal to zero to obtain the solution, which is  or . These answers are valid because they are in the domain.