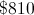Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : How to find direct variation

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find Direct Variation

If an object is hung on a spring, the elongation of the spring varies directly as the mass of the object. A 20 kg object increases the length of a spring by exactly 7.2 cm. To the nearest tenth of a centimeter, by how much does a 32 kg object increase the length of the same spring?

Possible Answers:

$4.5 \textrm{ cm}$

$9.1\textrm{ cm}$

$11.5 \textrm{ cm}$

$8.4 \textrm{ cm}$

$18.4 \textrm{ cm}$

Correct answer:

$11.5 \textrm{ cm}$

Explanation:

Let M,L be the mass of the weight and the elongation of the spring. Then for some constant of variation ,

L = kM

We can find by setting M = 20,L=7.2 from the first situation:

$7.2 = k \cdot 20$

$k = 7.2 \div 20 = 0.36$

so L = 0.36 M

In the second situation, we set M = 32 and solve for :

$L = 0.36 \cdot32 =11.52$

which rounds to 11.5 centimeters.

Report an Error

Example Question #1 : How To Find Direct Variation

varies directly with the square root of . If x = 25 , then y = 48 . What is the value of if x = 81 ?

Possible Answers:

155.52

86.4

$26\tfrac{2}{3}$

491.52

None of these answers are correct.

Correct answer:

86.4

Explanation:

If varies directly with the square root of , then for some constant of variation ,

$\small y = K \sqrt{x}$

If x = 25 , then y = 48 ; therefore, the equation becomes

$\small \small 48 = K \sqrt{25}$ ,

5K = 48 .

Divide by 5 to get K = 9.6 , making the equation

$\small \small y = 9.6 \sqrt{x}$ .

If x = 81 , then $\small \small \small y = 9.6 \sqrt{81} = 9.6 \cdot 9 = 86.4$ .

Report an Error

Example Question #2 : How To Find Direct Variation

If an object is hung on a spring, the elongation of the spring varies directly with the mass of the object. A 33 kilogram object increases the length of a spring by exactly 6.6 centimeters. To the nearest tenth of a kilogram, how much mass must an object posess to increase the length of that same spring by exactly 10 centimeters?

Possible Answers:

$80 \textrm{ kg}$

$200 \textrm{ kg}$

$100 \textrm{ kg}$

$40 \textrm{ kg}$

$50 \textrm{ kg}$

Correct answer:

$50 \textrm{ kg}$

Explanation:

Let M,L be the mass of the weight and the elongation of the spring, respectively. Then for some constant of variation ,

L = kM .

We can find by setting M = 33,L=6.6 :

$6.6 = k \cdot 33$

$k = 6.6 \div 33 = 0.2$

Therefore L = 0.2 M .

Set L = 10 and solve for :

10= 0.2 M

$M = 10 \div 0.2 = 50$ kilograms

Report an Error

Example Question #1 : How To Find Direct Variation

If is directly proportional to and when a=24 at b=12 , what is the value of the constant of proportionality?

Possible Answers:

2.5

1.5

Correct answer:

Explanation:

The general formula for direct proportionality is

a=kb

where is the proportionality constant. To find the value of this , we plug in a=24 and b=12

24=12k

Solve for by dividing both sides by 12

$\frac{24}{12}=\frac{12k}{12}$

2=k

So k=2 .

Report an Error

Example Question #3 : How To Find Direct Variation

The amount of money you earn is directly proportional to the nunber of hours you worked. On the first day, you earned $32 by working 4 hours. On the second day, how many hours do you need to work to earn $48.

Possible Answers:

Correct answer:

Explanation:

The general formula for direct proportionality is

M=kh

where is how much money you earned, is the proportionality constant, and is the number of hours worked.

Before we can figure out how many hours you need to work to earn $48, we need to find the value of . It is given that you earned $32 by working 4 hours. Plug these values into the formula

32=4k

Solve for by dividing both sides by 4.

$\frac{32}{4}=\frac{4k}{4}$

8=k

So k=8 . We can use this to find out the hours you need to work to earn $48. With k=8 , we have

M=8h

Plug in $48.

48=8h

Divide both sides by 8

$\frac{48}{8}=\frac{8h}{8}$

6=h

So you will need to work 6 hours to earn $48.

Report an Error

Example Question #4 : How To Find Direct Variation

The volume of a fixed mass of gas varies inversely as the atmospheric pressure, as measured in millibars, acting on it, and directly as the temperature, as measured in kelvins, acting on it.

A balloon is filled to a capacity of exactly 100 cubic meters at a time at which the temperature is 310 kelvins and the atmospheric pressure is 1,020 millibars. The balloon is released, and an hour later, the balloon is subject to a pressure of 900 millibars and a temperature of 290 kelvins. To the nearest cubic meter, what is the new volume of the balloon?

Possible Answers:

$121 \textrm{ m}^{3}$

$100 \textrm{ m}^{3}$

$94 \textrm{ m}^{3}$

$106 \textrm{ m}^{3}$

$83 \textrm{ m}^{3}$

Correct answer:

$106 \textrm{ m}^{3}$

Explanation:

If V,P,T are the volume, pressure, and temperature, then the variation equation will be, for some constant of variation ,

$V = \frac{KT}{P}$

To calculate , substitute V = 100, T = 310, P = 1,020 :

$100 = \frac{K \cdot 310}{1,020}$

$\frac{K \cdot 310}{1,020} \cdot \frac{1,020}{310} = 100 \cdot \frac{1,020}{310}$

K = 329.03

The variation equation is

$V = \frac{329.03 T}{P}$

so substitute T =290, P = 900 and solve for .

$V = \frac{329.03 \cdot 290}{900} \approx 106 \textrm{ m}^{3}$

Report an Error

Example Question #4 : How To Find Direct Variation

The monthly cost to insure your cars varies directly with the number of cars you own. Right now, you are paying $420 per month to insure 3 cars, but you plan to get 2 more cars, so that you will own 5 cars. How much does it cost to insure 5 cars monthly?

Possible Answers:

$\$748$

$\$700$

$\$810$

$\$633$

$\$390$

Correct answer:

$\$700$

Explanation:

The statement, 'The monthly costly to insure your cars varies directly with the number of cars you own' can be mathematically expressed as M=kC . M is the monthly cost, C is the number of cars owned, and k is the constant of variation.

Given that it costs $420 a month to insure 3 cars, we can find the k-value.

420=k * 3

Divide both sides by 3.

k=140

Now, we have the mathematical relationship.

M=140C

Finding how much it costs to insure 5 cars can be found by substituting 5 for C and solving for M.

M=140(5)

M=700

Report an Error

Example Question #211 : Functions And Lines

Does the equation below represent a direct variation? If it does, find the constant of variation.

7y = 2x

Possible Answers:

No, $y = \frac{1}{14}x, \frac{1}{14}$

Yes, y = 14x, 14

Yes, $y = \frac{2}{7}x$ $, \frac{2}{7}$

No, $\frac{7}{2}y = x$ , 1

Yes, $y= \frac{7}{2}x, \frac{7}{2}$

Correct answer:

Yes, $y = \frac{2}{7}x$ $, \frac{2}{7}$

Explanation:

Direct Variation is a relationship that can be represented by a function in the form

y = kx , where $k \neq 0$

is the constant of variation for a direct variation. is the coefficient of .

7y = 2x

$y = \frac{2}{7}x$

The equation is in the form y = kx , so the equation is a direct variation.

The constant of variation or is $\frac{2}{7}$

Therefore, the answer is,

Yes it is a direct variation, $y = \frac{2}{7}x,$ with a direct variation of $\frac{2}{7}$

Report an Error

Example Question #212 : Functions And Lines

Suppose x=24 and y=4 , and that is in direct proportion with . What is the value of proportionality?

Possible Answers:

$\frac{1}{6}$

5.5

Correct answer:

Explanation:

The general formula for direct proportionality is

x=ky

where is our constant of proportionality. From here we can plug in the relevant values for and to get

24=4k

Solving for requires that we divide both sides of the equation by , yielding

k=6

Report an Error

Example Question #5 : How To Find Direct Variation

The cost of a catering company varies directly with the number of people attending. If the cost is $100 when 20 people attend the party, find the constant of variation.

Possible Answers:

k=5

k=8

k=40

k=2000

Correct answer:

k=5

Explanation:

Because the cost varies directly with the number of people attending, we have the equation

C=kN

Where is the cost and is the number of people attending.

We solve for , the constant of variation, by plugging in C=100 and N=20 .

100=k(20)

And by dividing by 20 on both sides

$\frac{100}{20}=\frac{k(20) }{20}$

Yields

k=5

Report an Error

View Algebra Tutors

Tajrin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View Algebra Tutors

Alvin
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Computer Science.

View Algebra Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Atlanta, LSAT Tutors in San Diego, Spanish Tutors in Phoenix, Spanish Tutors in Seattle, ACT Tutors in Chicago, French Tutors in New York City, Reading Tutors in Chicago, Statistics Tutors in Chicago, GMAT Tutors in Chicago, Spanish Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Boston, SAT Courses & Classes in Phoenix, ACT Courses & Classes in San Diego, SAT Courses & Classes in Chicago, ISEE Courses & Classes in San Diego, GRE Courses & Classes in Seattle, SAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Washington DC, ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in San Diego, GMAT Test Prep in Seattle, GRE Test Prep in Boston, ACT Test Prep in Dallas Fort Worth, GRE Test Prep in Seattle, GMAT Test Prep in Washington DC, MCAT Test Prep in Houston, MCAT Test Prep in Denver, LSAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : How to find direct variation

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #1 : How To Find Direct Variation

Example Question #1 : How To Find Direct Variation

Example Question #2 : How To Find Direct Variation

Example Question #1 : How To Find Direct Variation

Example Question #3 : How To Find Direct Variation

Example Question #4 : How To Find Direct Variation

Example Question #4 : How To Find Direct Variation

Example Question #211 : Functions And Lines

Example Question #212 : Functions And Lines

Example Question #5 : How To Find Direct Variation

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: