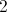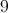$\displaystyle x+y=32$ rearranges to

$\displaystyle x=32-y$

and

$\displaystyle x=\frac{2}{3}y-2$, so

$\displaystyle 32-y=\frac{2}{3}y-2$

$\displaystyle 32-1\frac{2}{3}y=-2$

$\displaystyle -1\frac{2}{3}y=-34$

$\displaystyle -\frac{5}{3}y=-34$

$\displaystyle y=\frac{-34}{1}\cdot\frac{-3}{5}=\frac{102}{5}=20\frac{2}{5}$

$\displaystyle x=32-20\frac{2}{5}=11\frac{3}{5}$

In the second equation, you can substitute $\displaystyle 3x + 4$ for $\displaystyle y$ from the first.

$\displaystyle 2x + 3y = 34$

$\displaystyle 2x + 3 (3x + 4) = 34$

$\displaystyle 2x + 3 (3x) + 3 (4) = 34$

$\displaystyle 2x + 9x + 12 = 34$

$\displaystyle 11x + 12 = 34$

$\displaystyle 11x = 22$

$\displaystyle x = 2$

Now, substitute 2 for $\displaystyle x$ in the first equation:

$\displaystyle y = 3x + 4$

$\displaystyle y = 3 (2) + 4$

$\displaystyle y = 6 + 4$ 

$\displaystyle y = 10$

The solution is $\displaystyle (2, 10)$

To find the point where these two lines intersect, set the equations equal to each other, such that $\displaystyle y$ is substituted with the $\displaystyle x$ side of the second equation. Solving this new equation for $\displaystyle x$ will give the $\displaystyle x$-coordinate of the point of intersection.

$\displaystyle 3x = x - 2$

Subtract $\displaystyle x$ from both sides.

$\displaystyle (3x) - x = (x - 2) - x$

$\displaystyle 2x = - 2$

Divide both sides by 2.

$\displaystyle \frac{2x}{2} = \frac{-2}{2}$

$\displaystyle x = - 1$

Now substitute $\displaystyle -1$ into either equation to find the $\displaystyle y$-coordinate of the point of intersection.

$\displaystyle y = 3x$

$\displaystyle y= 3(-1)$

$\displaystyle y = -3$

With both coordinates, we know the point of intersection is $\displaystyle (-1,-3)$. One can plug in $\displaystyle -1$ for $\displaystyle x$ and $\displaystyle -3$ for $\displaystyle y$ in both equations to verify that this is correct.

$\displaystyle 3x - 5y = 5$

$\displaystyle -2x + 5y = 0$

Add the equations together.

$\displaystyle 3x+(-2x)=x$

$\displaystyle -5y+5y=0$

$\displaystyle 5+0=5$

Put the terms together to see that $\displaystyle x+0=5\ \textup{or}\ x=5$.

Substitute this value into one of the original equaitons and solve for $\displaystyle y$.

$\displaystyle 3x - 5y = 5$

$\displaystyle 3(5) - 5y = 5$

$\displaystyle -5y=-10$

$\displaystyle y=2$

Now we know that $\displaystyle x=5\ \textup{and}\ y=2$, thus we can find the sum of $\displaystyle x$ and $\displaystyle y$.

$\displaystyle x+y=5+2=7$

We can solve this problem by setting up a simple system of equations. First, we want to change the equations so one variable can cancel out. Multiplying the first equation by 2 and the second equation by 3 gives us a new system of $\displaystyle 2y = 6x + 8$ and $\displaystyle 3y=-6x+27$. These equations add up to $\displaystyle 5y=35$ or $\displaystyle y = 7$. Plugging in 7 for $\displaystyle y$ in either of the original two equations shows us that $\displaystyle x$ is equal to 1 and the point is $\displaystyle (1,7)$.

This system has infinite solutions becasue the two equations are actually the exact same line. To discover this, put both equations in terms of y.

First, $\displaystyle 2x - y = -3$. Add y to both sides:

$\displaystyle 2x = -3 + y$ Now add 3 to both sides:

$\displaystyle 2x + 3 = y$

Now we can show that the second equation also represents the line $\displaystyle y=2x + 3$

$\displaystyle 2y-6 = 4x$ add 6 to both sides

$\displaystyle 2y = 4x + 6$ divide both sides by 2

$\displaystyle y=2x+3$

Since both equations are the same line, literally any point on one line will also be on the other - infinite solutions.

A system of equations can be solved by subsituting one variable for another. Since we know that $\displaystyle y=x-2$, we can subsitute this into the other equation so $\displaystyle x-2=2x-4$. This expression can be solved to find that $\displaystyle x=-6$. Now that we know the value of $\displaystyle x$ it can be subsituted into either of the original equations to find $\displaystyle y$.

$\displaystyle \\\textup{Pig, Dog and Cat are } P, D, \textup{ and } C \textup{ years old, respectively.}\\\textup{The three statements translate in the following three equations, respectively}\\P-2=3(D-2)\\P+1=3(C+1)\\P+2=2.5(C+2).\\\textup{ Subtract the first from the second equation and obtain }\\(P-2)-(P+1)=(3D-6)-(3C+3)\\-3=3(D-C)-9\\D-C=2.\\\textup{So Dog is two years older than Cat.}$

To find the intersection point, you must find the values of x and y that satisfy the two equations. We can use the method of adding the two equations together:

$\displaystyle 3x+ 2y=4$

$\displaystyle 5x-2y=4$

If we add the equations together, the y terms cancel out, so we get

$\displaystyle 8x=8$

$\displaystyle x=1$

Now that we know the value of x, we can plug that into one of the equations and solve for y. Pluggin it into the first equation, we get

$\displaystyle 3(1)+2y=4$

$\displaystyle 2y=1$

$\displaystyle y=\frac{1}{2}$.

So that point of intersection is $\displaystyle (x,y)$, or $\displaystyle \left(1,\frac{1}{2}\right)$.

There are several methods to find the solution set to this system of equations, but here we will use the substitution method for its ease of application. The idea of this method is to solve one of the equations (and you can choose either) in terms of one variable and then plug it into the second equation that was not tampered with to solve it for the other variable. Do not worry if this isn't completely clear just yet. But after you read the step-by-step solution review this paragraph and make sure the math language and this explanation align in your mind.

1) $\displaystyle 3x-6y=9$

2) $\displaystyle 2y+4x=8$

First solve equation 2 for y. Again, it is your choice which equation and which variable to use, but try and select one that will take the least work. In our case neither are "better", but the bottom equation will not yield a fraction.

$\displaystyle 2y+4x=8$

move over x term

$\displaystyle 2y=-4x+8$

isolate y

$\displaystyle y=-2x+4$

Now we have equation 2 in terms of one variable (y=....). We must now plug this equation we just made back into one of the original equations to solve that equation for one variable. Let's do equation 1:

$\displaystyle 3x-6(-2x+4)=9$

Notice how all we've done is replace the y in equation 1 with the modified version of equation 2. Now solve for x:

Simplify the parenthesis:

$\displaystyle 3x+12x-24=9$

Combine x's and move the constant over:

$\displaystyle 15x=33$

$\displaystyle x=2.2$

Now we have solved for one variable and are almost done! Plug this value into either original equation and solve for y. Let's plug it into equation 2:

$\displaystyle 2y+4(2.2)=8$

move the constant over after simplifying:

$\displaystyle 2y=-.8$

$\displaystyle y=-0.4$

Final answer= $\displaystyle (2.2,-0.4)$

We now have solved for each variable. Thus our solution set to this system of equations, where they are equal to each other, or where their lines intersect is (2.2,-0.4)! Since there are multiple ways to solve this problem, there are mutiple ways to check yourself. Convert both equations to slope intercept form, graph them using a graphing utility, and use the trace or intersect function to see that these two lines really do intersect and therefore equal each other at this coordinate point. Alternately just plug in the coordinate pair to either ORIGINAL equation, but the graphical method is probably easy since we have decimals.