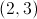Call Now to Set Up Tutoring:

(888) 888-0446

Algebra 1 : Systems of Equations

Study concepts, example questions & explanations for Algebra 1

Create An Account

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #161 : Systems Of Equations

Solve for :

7x+3-2x=x+11

Possible Answers:

Correct answer:

Explanation:

First, combine like terms to get 5x+3=x+11 .

Then, subtract 3 and from both sides to get 4x=8 .

Then, divide both sides by 2 to get a solution of x=4 .

Report an Error

Example Question #42 : Equations / Solution Sets

Solve this system of equations:

3x+5y=-11

9x-5y=-1

Possible Answers:

$\left(-1,\frac{8}{5}\right)$

$\left ( 1,\frac{8}{5} \right )$

$\left(0,1 \right )$

$\left ( -3,1 \right )$

$\left ( 5,1 \right )$

Correct answer:

$\left(-1,\frac{8}{5}\right)$

Explanation:

To solve this system of equations, the elimination method can be used (the terms cross out).

Once you eliminate the y's , you have 12x=-12 .

Then isolate for , and you get x=-1 .

Plug into the first equation to solve for .

3(-1)+5y=-11

-3+5y=-11

-3+5y+3=-11+3

5y=-8

$\frac{5y}{5}=\frac{-8}{5}$

$y=-\frac{8}{5}$

Report an Error

Example Question #162 : Systems Of Equations

Solve the following system of equations:

4x - 2y = 14

6y -12x = -42

Possible Answers:

$x=2,\ y=-3$

This system has no solution.

This system has an infinite number of solutions.

$x=5,\ y=6$

$x=-3,\ y=2$

Correct answer:

This system has an infinite number of solutions.

Explanation:

Rearrange the second equation:

$6y -12x = -42 \Rightarrow 12x - 6y = 42$

This is just a multiple of the first equation (by a factor of 3). Therefore, the two equations are dependent on each are and are going to have an infinite number of solutions.

Report an Error

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve the set of equations:

3x+2y=12

4x-3y=-1

Possible Answers:

$\left ( 2,3 \right )$

$\left ( -1,-1 \right )$

$\left ( 1,1 \right )$

$\left ( 4,0 \right )$

Correct answer:

$\left ( 2,3 \right )$

Explanation:

Solve the first equation for :

3x+2y=12

2y=12-3x

$y=6-\frac{3}{2}x$

Substitute into the second equation:

$4x-3(6-\frac{3}{2}x)=-1$

$4x-18+\frac{9}{2}x=-1$

Multiply the entire equation by 2 to eliminate the fraction:

8x-36+9x=-2

17x-36=-2

17x=34

x=2

Using the value of , solve for :

3(2)+2y=12

6+2y=12

2y=6

y=3

Therefore, the solution is $\left ( 2,3 \right )$

Report an Error

Example Question #2 : Systems Of Equations

Find the solution:

3x+2y=12

-2x+3y=5

Possible Answers:

x=6, y=3

x=3, y=6

x=3, y=2

x=-2, y=-3

x=2, y=3

Correct answer:

x=2, y=3

Explanation:

To solve this system of equations, we must first eliminate one of the variables. We will begin by eliminating the variables by finding the least common multiple of the variable's coefficients. The least common multiple of 3 and 2 is 6, so we will multiply each equation in the system by the corresponding number, like

2(3x+2y=12)

3(-2x+3y=5) .

By using the distributive property, we will end up with

6x+4y=24

-6x+9y=15

Now, add down each column so that you have

$0x+13y=39 \rightarrow 13y=39$

Then you solve for and determine that y=3 .

But you're not done yet! To find , you have to plug your answer for back into one of the original equations:

3x+2(3)=12

Solve, and you will find that x=2 .

Report an Error

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Solve the following system of equations:

y = 2x-2

y = 3x+6

Possible Answers:

x=4,y=16

x=-4,y=-10

x=-8, y=-18

x=-4,y=-6

x=8,y=14

Correct answer:

x=-8, y=-18

Explanation:

Set the two equations equal to one another:

2x - 2 = 3x + 6

Solve for x:

x = -8

Plug this value of x into either equation to solve for y. We'll use the top equation, but either will work.

y = 2 * (-8) - 2

y = -18

Report an Error

Example Question #163 : Systems Of Equations

Solve the following system of equations:

3x+2y = 8

x - 2y = 4

Possible Answers:

x=3, y=-2

x=2,y=1

x=-2,y=1

x=3, y=-0.5

x=3,y=-1

Correct answer:

x=3, y=-0.5

Explanation:

Solve the second equation for y:

x - 2y = 4

-2y = 4 - x

y = -2 + x/2

Plug this into the first equation:

3x + 2(-2 + x/2) = 8

Solve for x:

3x - 4 + x = 8

4x = 12

x = 3

Plug this into the second equation to get a value for y:

3 - 2y = 4

2y = -1

y = -0.5

Report an Error

Example Question #164 : Systems Of Equations

Solve the following system of equation

-4x-2y+z=7

9y-5z=-8

6 z=-12

Possible Answers:

$(x,y,z)=\left (-2,2,-\frac{5}{4} \right )$

Cannot be solved

$(x,y,z)=\left (-5,-3,-4} \right )$

$(x,y,z)=\left (-\frac{7}{2},-9,-8 \right )$

$(x,y,z)=\left (-\frac{5}{4},-2,-2 \right)$

Correct answer:

$(x,y,z)=\left (-\frac{5}{4},-2,-2 \right)$

Explanation:

Start with the equation with the fewest variables, $\ 6z=-12$ .

Solve for by dividing both sides of the equaion by 6:

$\frac{6z}{6}=\frac{-12}{6}$

z=-2

Plug this value into the second equation to solve for :

9y-5z=-8

9y-5(-2)=-8

9y+10=-8

Subtract 10 from both sides:

9y+10-10=-8-10

9y=-18

Divide by 9:

$\frac{9y}{9}=\frac{-18}{9}$

y=-2

Plug these and values into the first equation to find :

-4x-2(-2)+(-2)=7

-4x+4-2=7

Combine like terms:

-4x+2=7

Subtract 2:

-4x+2-2=7- 2

-4x=5

Divide by -4:

$\frac{-4x}{-4}=\frac{5}{-4}$

$x=-\frac{5}{4}$

Therefore the final solution is $(x,y,z)=\left (-\frac{5}{4},-2,-2 \right)$ .

Report an Error

Example Question #165 : Systems Of Equations

Two integers, and , sum to 16, but when is doubled, they sum to 34. Find and .

Possible Answers:

(x,y)=(2,-9)

(x,y)=(18,-2)

(x,y)=(0,-4)

No solution

(x,y)=(-4,8)

Correct answer:

(x,y)=(18,-2)

Explanation:

and add up to 16: x+y=16

When is doubled to , they sum to 34: 2x+y=34

We have two equations and two unknowns, so we can find a solution to this system.

Solve for in the first equation:

x=16-y

Plug this into the second equation:

2(16-y)+y=34

Solve for :

32-2y+y=34

32-y=34

-y=2

y=-2

Use this value to find . We already have a very simple equation for , x=16-y .

x=16-(-2)

x=18

Therefore the answer is (x,y)=(18,-2) .

Report an Error

Example Question #261 : Equations / Inequalities

Solve for .

4x+3y=6

2x+2y=4

Possible Answers:

x=-2

$x=\frac{3}{4}$

x=0

x>0

x=2

Correct answer:

x=0

Explanation:

4x+3y=6

2x+2y=4

For the second equation, solve for in terms of .

4-2x=2y

y=2-x

Plug this value of y into the first equation.

4x+3(2-x)=6

4x + 6- 3x =6

x=0

Report an Error

View Algebra Tutors

Eashan
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Computer Science.

View Algebra Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Algebra Tutors

Joseph
Certified Tutor

Old Dominion University, Bachelor of Science, Electrical Engineering. Western Governors University, Masters in Education, Mat...

All Algebra 1 Resources

10 Diagnostic Tests 557 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Los Angeles, SSAT Tutors in Washington DC, MCAT Tutors in Washington DC, ISEE Tutors in Boston, Statistics Tutors in San Francisco-Bay Area, Reading Tutors in New York City, French Tutors in San Diego, GRE Tutors in Seattle, Math Tutors in Dallas Fort Worth, MCAT Tutors in Chicago

Popular Courses & Classes

Spanish Courses & Classes in Washington DC, GMAT Courses & Classes in Denver, Spanish Courses & Classes in Philadelphia, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Houston, ACT Courses & Classes in Los Angeles, ISEE Courses & Classes in Seattle, ACT Courses & Classes in Phoenix, SAT Courses & Classes in San Diego, GMAT Courses & Classes in New York City

Popular Test Prep

GRE Test Prep in Seattle, MCAT Test Prep in Atlanta, GRE Test Prep in Atlanta, GRE Test Prep in San Diego, LSAT Test Prep in Philadelphia, SSAT Test Prep in Philadelphia, GRE Test Prep in Philadelphia, ACT Test Prep in Miami, GMAT Test Prep in New York City, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra 1 : Systems of Equations

Study concepts, example questions & explanations for Algebra 1

All Algebra 1 Resources

Example Questions

Example Question #161 : Systems Of Equations

Example Question #42 : Equations / Solution Sets

Example Question #162 : Systems Of Equations

Example Question #1 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #2 : Systems Of Equations

Example Question #2 : Solve Systems Of Two Linear Equations: Ccss.Math.Content.8.Ee.C.8b

Example Question #163 : Systems Of Equations

Example Question #164 : Systems Of Equations

Example Question #165 : Systems Of Equations

Example Question #261 : Equations / Inequalities

All Algebra 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: