Call Now to Set Up Tutoring:

(888) 888-0446

Advanced Geometry : Plane Geometry

Study concepts, example questions & explanations for Advanced Geometry

Create An Account

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Plane Geometry

$\small \small Find\ the\ height\ of\ a\ trapezoid\ with\ bases\ of\ 8\ and\ 12\ and\ an\ area\ of\ 80m^{2}.$

Possible Answers:

$\small 12\ m$

$\small 60\ m$

$\small \small \small 10\ m$

$\small \small 8\ m$

Correct answer:

$\small \small 8\ m$

Explanation:

$\small Use\ the\ area\ formula\ for\ a\ trapezoid.$

$\small A=\frac{b_{1}+b_{2}}2(h)$

$\small Substitute\ each\ known\ value\ then\ use\ algebra\ to\ solve\ for\ the\ height.$

$\small \small 80=\frac{8+12}{2}h$

$\small 80=10h$

$\small 8=h$

Report an Error

Example Question #352 : Advanced Geometry

Find the area of the trapezoid given below:

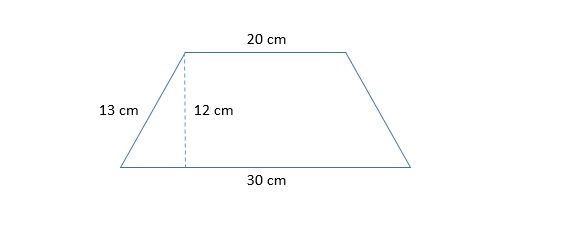
Trap1

Possible Answers:

$300\ cm^2$

$325\ cm^2$

$240\ cm^2$

$260\ cm^2$

Correct answer:

$300\ cm^2$

Explanation:

In order to find the area of a trapezoid, we must use the formula below:

$A=\frac{b_{1}+b_{2}}{2}(h)$

$In\ this\ trapezoid\ b_{1}=30\ and\ b_{2}=20.$

$We\ can\ also\ see\ that\ h=12.$

$When\ we\ plug\ in\ all\ of\ the\ above\ values\ into\ the\ formula\ we\ get:$

$A=\frac{20+30}{2}(12)$

A=300cm^2

Report an Error

Example Question #16 : Trapezoids

Show algebraically how to develop the trapezoid area formula.

Varsity7

Possible Answers:

$\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

$h(b_{1}\cdot b_{2})$

$= \frac{1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

$\frac{1}{2}(b_{1}+b_{2})+h$

$= \frac{h}{2}(b_{1}+b_{2})$

$\frac{1}{2}(b_{1}+b_{2})+h$ $\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{h}{2}(b_{1}+b_{2})$

$h^{2}(\frac{1}{2}b_{1}+\frac{1}{2}b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Correct answer:

$\frac{1}{2}b_{1}h+\frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Explanation:

1) The area $A_{1}$ of the triangle that has base $b_{1}$ is $A_{1} = \frac{1}{2}(b_{1})h$ .

2) The area $A_{2}$ of the triangle that has base $b_{2}$ is $A_{2} = \frac{1}{2}(b_{2})h$ .

3) The sum of the two triangel areas is

$A_{1} + A_{2}$

$= \frac{1}{2}b_{1}h + \frac{1}{2}b_{2}h$

$= \frac{1}{2}(b_{1}h+b_{2}h)$

$= \frac{1}{2}h(b_{1}+b_{2})$

$= \frac{h\cdot 1}{2}(b_{1}+b_{2})$

$= \frac{h}{2}(b_{1}+b_{2})$

Report an Error

Example Question #21 : How To Find The Area Of A Trapezoid

Find the area of the trapezoid.

Varsity2

Possible Answers:

For area ,

$A = \frac{h}{2}(b_{1} + b_{2})$

$= \frac{2a}{2}(a + 4a)$

= a(5a)

$= 5a^{2}$

$A = \frac{1}{2}(a + 2a)$

$= \frac{1}{2}(3a)$

$A = a\cdot2a\cdot4a$

$= 8a^{3}$

$A = 4\cdot \frac{1}{2}(4a-a)2a$

$= 4\cdot \frac{1}{2}(3a)2a$

$= 2\cdot3a\cdot2a$

$= 12a^{2}$

$A = \frac{1}{2}\cdot4a\cdot2a + a$

$= 4a^{2} + a$

$= 5a^{2}$

Correct answer:

For area ,

$A = \frac{h}{2}(b_{1} + b_{2})$

$= \frac{2a}{2}(a + 4a)$

= a(5a)

$= 5a^{2}$

Explanation:

1) Using the trapezoid area formula, $A = \frac{h}{2}(b_{1} + b_{2})$ ,

height h = 2a , base $b_{1} = a$ , base $b_{2} = 4a$ .

2) After substition, the resulting expression is $= \frac{2a}{2}(a + 4a)$ .

3) The resulting expression is then simplified,

= a(5a)

$= 5a^{2}$

Report an Error

Example Question #22 : Trapezoids

The rectangle is circumscribed about the trapezoid EBCF . Find the area $A_{T}$ of the trapezoid.

Varsity6

Possible Answers:

49.56

37.5

Correct answer:

49.56

Explanation:

1) The measure of the trapezoid top base $\overline{BC}$ has to be found.

2) To find $m(\overline{BC})$ , and have to be found, then the sum x + y is subtracted from the length of the top side of the rectangle, resulting in the difference 10 - (x + y) .

3) $m(\overline{BC}) = 10 - (x + y)$ .

3) By using the Pythagorean Theorem on $\bigtriangleup EAB$ and $\bigtriangleup FCD$ , and can be found.

4) Using $\bigtriangleup EAB$ for ,

$(7.5)^{2} + x^{2} = 8^{2}$

$x^{2} = 64 - 56.25$

$x^{2} = 7.75$

$x = \sqrt{7.75}$

$x \approx 2.784$

5) Using $\bigtriangleup FCD$ for ,

$(7.5)^{2} + y^{2} = (8.5)^{2}$

$y^{2} = 72.25 - 56.25$

$y^{2} = 16$

y = 4

6) $BC = 10 - (\sqrt{7.75} + 4) \approx 3.216$

7) $A_{T} = \frac{7.5}{2} \cdot ( 3.216 + 10)$

= (3.75)(13.216)

= 49.56

Report an Error

Example Question #22 : How To Find The Area Of A Trapezoid

Find the area of the shaded region.

Varsity3

Possible Answers:

105

322

22.5

200

Correct answer:

22.5

Explanation:

The shaded region is between the outer and inner trapezoid. To find the area of the shaded region, subtract the area of the inner trapezoid from the area of the outer trapezoid.

1) Area of the shaded region = $A_{S}$ , area of the outer trapezoid = $A_{O}$ , area of the inner trapezoid = $A_{I}$ .

2) $A_{O} = \frac{5}{2}(5 + 10)$ , $A_{I} = \frac{3}{2}(4 + 6)$

3) $A_{S} = A_{O} - A_{I}$

$= \frac{5}{2}(5 + 10) - \frac{3}{2}(4 + 6)$

$= \frac{5}{2}(15) - \frac{3}{2}(10)$

$= \frac{75}{2} - \frac{30}{2}$

$= \frac{45}{2}$

= 22.5

Report an Error

Example Question #23 : How To Find The Area Of A Trapezoid

Find the area of the figure.

Possible Answers:

82.83

79.06

81.27

85.33

Correct answer:

82.83

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{6^2+12^2}=\sqrt{180}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(10+\sqrt{180})(4)=20+2\sqrt{180}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(6)(12)=36$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=20+2\sqrt{180}+36=82.83$

Make sure to round to places after the decimal.

Report an Error

Example Question #25 : Trapezoids

Find the area of the figure.

Possible Answers:

Correct answer:

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{5^2+12^2}=\sqrt{169}=13$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(11+13)(3)=36$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(5)(12)=30$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=30+36=66$

Report an Error

Example Question #26 : Trapezoids

Find the area of the figure below.

Possible Answers:

136.28

150.09

164.67

114.00

Correct answer:

164.67

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{10^2+16^2}=\sqrt{356}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(15+\sqrt{356})(5)=\frac{75+5\sqrt{356}}{2}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(10)(16)=80$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=\frac{75+5\sqrt{356}}{2}+80=164.67$

Make sure to round to places after the decimal.

Report an Error

Example Question #27 : Trapezoids

Find the area of the figure.

Possible Answers:

75.64

68.09

64.63

71.22

Correct answer:

64.63

Explanation:

From the figure, you should notice that it is made up of a right triangle and a trapezoid. The lower base of the trapezoid is also the hypotenuse of the right triangle.

First, find the length of the hypotenuse of the right triangle using the Pythagorean Theorem.

$\text{Hypotenuse}=\sqrt{\text{base}^2+\text{height}^2}$

$\text{Hypotenuse}=\sqrt{6^2+9^2}=\sqrt{117}$

Next, use this value to find the area of the trapezoid.

$\text{Area of Trapezoid}=\frac{1}{2}(\text{base 1}+\text{base 2})(\text{height})$

Plug in the given and found values to find the area.

$\text{Area of Trapezoid}=\frac{1}{2}(8+\sqrt{117})(4)=16+2\sqrt{117}$

Next, find the area of the triangle.

$\text{Area of Triangle}=\frac{1}{2}(\text{base})(\text{height})$

$\text{Area of Triangle}=\frac{1}{2}(6)(9)=27$

To find the area of the figure, add the two areas together.

$\text{Area of Figure}=\text{Area of Trapezoid}+\text{Area of Triangle}$

$\text{Area of Figure}=16+2\sqrt{117}+27=64.63$

Make sure to round to places after the decimal.

Report an Error

View Tutors

Monica
Certified Tutor

Bloomsburg University of Pennsylvania, Bachelor of Education, Language Arts Teacher Education. Lehigh University, Masters in ...

View Tutors

Ruting
Certified Tutor

dalian martime university, Bachelor in Business Administration, Public Administration. university of ottwa, Master of Arts, P...

View Tutors

Alan
Certified Tutor

Michigan Technological University, Bachelor of Science, Mechanical Engineering. Michigan Technological University, Master of ...

All Advanced Geometry Resources

6 Diagnostic Tests 57 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in San Diego, ACT Tutors in Houston, GRE Tutors in Seattle, LSAT Tutors in Houston, GMAT Tutors in Boston, Physics Tutors in Boston, Chemistry Tutors in Seattle, GMAT Tutors in Washington DC, SSAT Tutors in Chicago, MCAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

SAT Courses & Classes in Houston, LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Atlanta, ACT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Phoenix, SAT Courses & Classes in Phoenix, MCAT Courses & Classes in Washington DC, GRE Courses & Classes in Miami, SAT Courses & Classes in Boston, Spanish Courses & Classes in Dallas Fort Worth

Popular Test Prep

SAT Test Prep in Seattle, SSAT Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Phoenix, MCAT Test Prep in Miami, ACT Test Prep in Seattle, ISEE Test Prep in Denver, SAT Test Prep in Atlanta, GRE Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Advanced Geometry : Plane Geometry

Study concepts, example questions & explanations for Advanced Geometry

All Advanced Geometry Resources

Example Questions

Example Question #61 : Plane Geometry

Example Question #352 : Advanced Geometry

Example Question #16 : Trapezoids

Example Question #21 : How To Find The Area Of A Trapezoid

Example Question #22 : Trapezoids

Example Question #22 : How To Find The Area Of A Trapezoid

Example Question #23 : How To Find The Area Of A Trapezoid

Example Question #25 : Trapezoids

Example Question #26 : Trapezoids

Example Question #27 : Trapezoids

All Advanced Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: