All Advanced Geometry Resources
Example Questions
Example Question #31 : Trapezoids
Find the length of both diagonals of this quadrilateral.
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:
Using Pythagorean Theorem gives:

Similarly, the other diagonal can be found with this right triangle:
Once again using Pythagorean Theorem gives an answer of
Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid
Find the length of the diagonals of this isosceles trapezoid, with 
To find the length of the diagonals, split the top side into 3 sections as shown below:
The two congruent sections plus 8 adds to 14. 

We can solve for the diagonal, now pictured, using Pythagorean Theorem:

Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid
Find the length of the diagonal of the isosceles trapezoid given below.
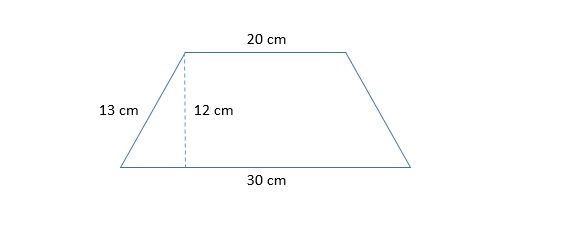
In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.
Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.

We now take the square root of both sides:
Example Question #1 : How To Find The Length Of The Diagonal Of A Trapezoid
Find the length of diagonal 

1) The diagonal 

2) The length of the base of 



3) 
4) Using the Pythagorean Theorem on 

5) Using the Pythagorean Theorem on 

Example Question #85 : Quadrilaterals

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

Example Question #2 : How To Find The Length Of The Diagonal Of A Trapezoid

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

Example Question #41 : Trapezoids

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 45-45-45 Triangle Theorem,
and


Set 

Example Question #1 : How To Find The Area Of A Rhombus
Which of the following shapes is a rhombus?

A rhombus is a four-sided figure where all sides are straight and equal in length. All opposite sides are parallel. A square is considered to be a rhombus.
Example Question #2 : How To Find The Area Of A Rhombus
Assume quadrilateral 


Solving for the area of rhombus 



The area of rhombus 

Example Question #3 : How To Find The Area Of A Rhombus

What is the area of the rhombus above?
The formula for the area of a rhombus from the diagonals is half the product of the diagonals, or in mathematical terms:



Substituting our values yields,
Certified Tutor
All Advanced Geometry Resources
























































































































