Chemists can model how solids, liquids, and gases behave at different temperatures and pressures with a graph called a phase diagram. When the pressure and temperature are simultaneously known, a scientist can predict whether the material will be in a specific state. The diagram is divided into sections depending on the phase and the lines between sections represent phase transitions occurring between two or more separate phases.

In general, solids of neatly stacked molecules exist when temperatures are low and pressures are intermediate. These values decrease the kinetic energy of the molecules enough to allow for attractive forces to begin the stacking process. Liquids, by contrast, are found at intermediate pressures and temperatures. The temperature is high enough to impart enough kinetic energy to prevent solid formation and the pressure is high enough to prevent the liquid from becoming a gas. Finally, a gas forms at low pressures and high temperatures. The high level of kinetic energy prevents molecules from associating with one another.

Materials can undergo processes called phase transitions, meaning they can transition from one phase to another. The transition from a solid to a liquid is called melting, while the reverse transition is called freezing. Vaporization occurs when a liquid becomes a gas, while condensation occurs when a gas becomes a liquid. Finally, in a process called sublimation, a solid can directly become a gas without passing through a liquid phase. Additionally, when a gas directly becomes a solid, this is known as deposition. 

At point B, a material is transitioning from its phase in area three to its phase in area two. What is this phase transition called?

If a drug is taken orally, then the concentration of that drug in the blood will rise to a peak concentration. Immediately afterwards, the elimination phase begins and the concentration of the drug in the body will fall exponentially. Each drug has a half-life (i.e. the time required for the drug's concentration in the blood to fall to half of its original value). Once the elimination phase has initiated, it typically takes four half-lives until the drug has been entirely eliminated from the body.

If an individual is given multiple doses of a drug over time, then the blood concentration of the drug will rise and fall periodically. This creates a graph of drug’s concentration versus time that will resemble a wave. The rising peaks of the graph occur immediately after administration of a dose, whereas the falling valleys occur as the drug is being eliminated. The inter-dose interval, represented by the letter , is defined as the time (in hours) between doses of the drug.

Experiment 1

A 125-milligram oral dose of a drug known as Cyclosporin A (CsA) was administered to an individual. The CsA blood concentration for this individual was then measured at various times over the next 24 hours. A graph of CsA concentration versus time was obtained.

Experiment 2

An individual was given multiple doses of CsA over a 60-hour period. The CsA blood concentration was monitored continuously. A graph of CsA concentration versus time was obtained.

If a drug’s concentration rises above a toxicity level at any point during administration, then unwanted side effects will occur. Suppose the toxicity level of CsA is as follows:

Based on the results of Experiment 2, did the individual receiving CsA experience unwanted side effects?

A botanist is trying to see the effects of temperature on a certain plant species. She prepares four identical plots of soil and runs a heating element through the soil so she can vary the temperature of each plot. After one month she harvests all of the plant biomass and records the temperature of each plot along with the biomass collected. The data are given in the table below.

After the experiment, the botanist noticed that the heating element was not calibrated properly and displayed a temperature 3 degrees lower than it actually was.

Given that the botanist's equipment was improperly calibrated, which temperature should he recommend to farmers who wish to have the highest yield?

Clock reactions are chemical interactions that exhibit a physical change periodically over a given time interval. Many of these reactions involve iodine, the most famous being the Chlorine Dioxide-Iodine-Malonic Acid reaction. These reactions can be quite startling as flasks of colorless liquid periodically turn dark blue and then resolve back to their original colorless state. Even more striking, they seem to alternate between being colorless and blue several times. The term "clock reaction" is derived from the fact that the time at which these sudden changes occur can be predicted. 

Beyond performing these reactions in a well stirred beaker, there are two other notable ways to conduct experiments with clock reactions that demonstrate interesting properties of these reactions. The first is in a continuous flow stirred tank reactor (CSTR). In a CSTR, the reactants are introduced at a continuous rate while the volume of liquid in the reactor is kept constant by siphoning off excess fluid. The result of this process is that one can maintain the ideal conditions in which the reaction may occur over time and restricts the buildup of excess product or reactant that would otherwise make the oscillations of the reactions decay. In a CSTR, clock reactions can be maintained switching predictably from colorless to blue, for example, for far longer than in a simple beaker.

The second way to conduct a clock reaction experiment is in a tank with no stirring at all. This allows the reactants to interact heterogeneously, or without being thoroughly mixed. When this occurs, we can get some parts of the tank that are one color and other parts that are another color. This means that we can observe two different stages of the reaction in one vessel. The patterns that this makes are called Turing patterns, named by the great computer scientist Alan Turing. Turing predicted that the heterogeneous mixing of chemicals called morphogens in complex organisms were responsible for biological pattern formation like spots on a leopard, stripes on a zebra, or patterns on a tropical fish. The existence of such patterns and chemicals has since been confirmed and clock reactions are often used to study these types of Turing patterns.

Based on the passage, which of the following researchers would most likely have studied clock reactions in their work?

An undergraduate biology student working in a lab was reading about the latest health epidemic in the United States concerning obesity. He recently learned in his biology class that an enzyme called fatty acid synthase (FAS) catalyzes the formation of fatty acids. Accumulation of these fatty acids then creates the adipose fatty tissue that individuals typically see in their belly or side-regions. He hypothesizes that by decreasing the rate that this enzyme produces fatty acids by administering an inhibitor will aid in reducing the storage of fats, helping to alleviate obesity. After gaining approval from the university's clinical trials and ethics committee, he gathered a group of 20 test subjects. With the help of his research director, he measured the baseline rate of FAS activity for all test subjects and the averaged rate after oral administrators of a placebo and three types of inhibitors at a concentration of 0.6M to four equally-sized groups. The data is shown in Table 1.                      

Table 1.

The student then wonders if a mixture of different inhibitors were to increase the effect in the subject. He again measured the averaged baseline FAS level of the subjects and then attempted administering a placebo and three different combinations of inhibitors to subjects in a second trial. The results are shown in Table 2.

Table 2. 

A colleague of the researcher interpreted the results from Table 1 and 2 and suggested a third trial which would track the averaged weight change of the subjects over a 6-month period. The results are shown in Table 3.

Table 3.

Given the change in weight loss over the six-month period, does the data of Table 3 correlate with the change in FAS activity with the administration of the drugs?

An undergraduate biology student working in a lab was reading about the latest health epidemic in the United States concerning obesity. He recently learned in his biology class that an enzyme called fatty acid synthase (FAS) catalyzes the formation of fatty acids. Accumulation of these fatty acids then creates the adipose fatty tissue that individuals typically see in their belly or side-regions. He hypothesizes that by decreasing the rate that this enzyme produces fatty acids by administering an inhibitor will aid in reducing the storage of fats, helping to alleviate obesity. After gaining approval from the university's clinical trials and ethics committee, he gathered a group of 20 test subjects. With the help of his research director, he measured the baseline rate of FAS activity for all test subjects and the averaged rate after oral administrators of a placebo and three types of inhibitors at a concentration of 0.6M to four equally-sized groups. The data is shown in Table 1.                      

Table 1.

The student then wonders if a mixture of different inhibitors were to increase the effect in the subject. He again measured the averaged baseline FAS level of the subjects and then attempted administering a placebo and three different combinations of inhibitors to subjects in a second trial. The results are shown in Table 2.

Table 2. 

A colleague of the researcher interpreted the results from Table 1 and 2 and suggested a third trial which would track the averaged weight change of the subjects over a 6-month period. The results are shown in Table 3.

Table 3.

Suppose that the researcher improperly mixed the Inhibitor II + III pills in the third experiment with Inhibitor I + III pills. What would be a reasonable change in weight that would be expected?

The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.

Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.

Figure 1:

By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.

Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified. 

Figure 2:

When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation: 

Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.

Table 1: 

The decision to use oil drops in Millikin's experiment was made after water drops were found to evaporate too quickly.  

Another scientist conducts an experiment and places two beakers into sealed chambers within a single larger, constant pressure chamber, as in the figure below. The pressure and temperature conditions in the chambers are all very similar to the conditions used in the Millikin experiment from the passage, without a vacuum.  

One beaker contains oil, and one beaker contains water. The volumes of both beakers are identical. Based on the information in the original passage, which of the following is most likely true:

The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.

Millikin used an experimental setup like the one shown in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.

Figure 1

By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.

Using this information, Millikin was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified. 

Figure 2

When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation: 

Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.

Table 1

A stronger electric field is needed to keep the oil drop in the field when a vacuum is used. This is most likely due to:

A student performed the following procedures to study various photosynthetic pigments (light-absorbing chemicals) in tree leaves and the wavelengths of light they absorb.

Experiment 1:

The student obtained samples of leaves from oaks, maples, ashes, sycamores, and poplars. Each leaf sample was ground separately with a mortar and pestle to release the pigments, and then each sample was suspended in water to make a colored solution of the pigment. The student then measured the absorption spectrum (a graph of how much light is absorbed by a pigment at varying wavelengths of light) of each solution in a device called a spectrophotometer. The setup of a spectrophotometer is shown below in Diagram 1.

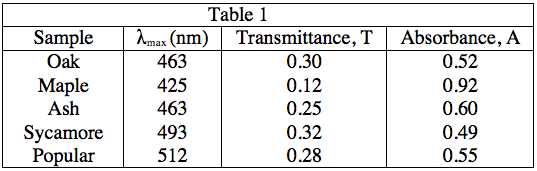
The light source emits white light, which is split into its various wavelengths by the prism. Next, a slit, which can be moved up or down to select a particular wavelength, is used to transmit just a single wavelength to the sample. The sample absorbs a fraction of this light that is characteristic to the pigment in the sample, and the rest is transmitted to the detector for a readout. Using the spectrophotometer, the student found the λ_max (the wavelength of light in nanometers (nm) that the pigment absorbs most intensely, for each sample) and recorded the results in Table 1. Table 1 also shows the transmittance and absorbance values at λ_max. Transmittance, T, is defined as the fraction of light, expressed as a decimal, which passes through the sample. Absorbance, A, is given by:

                                    A = –log(T)   or  10^–A = T

Experiment 2:

A student is given a leaf from an unknown source. She crushes and extracts the pigment according to the procedure in Experiment 1. Measuring the absorbance spectrum in the spectrophotometer produces the following readout, shown in Diagram 2.

                                                     Diagram 2

A lumberjack wants to plant trees that make the most efficient use of sunlight in a shady area of her land. Which trees should she plant?

A student performed the following procedures to study various photosynthetic pigments (light-absorbing chemicals) in tree leaves and the wavelengths of light they absorb.

Experiment 1:

The student obtained samples of leaves from oaks, maples, ashes, sycamores, and poplars. Each leaf sample was ground separately with a mortar and pestle to release the pigments, and then each sample was suspended in water to make a colored solution of the pigment. The student then measured the absorption spectrum (a graph of how much light is absorbed by a pigment at varying wavelengths of light) of each solution in a device called a spectrophotometer. The setup of a spectrophotometer is shown below in Diagram 1.

The light source emits white light, which is split into its various wavelengths by the prism. Next, a slit, which can be moved up or down to select a particular wavelength, is used to transmit just a single wavelength to the sample. The sample absorbs a fraction of this light that is characteristic to the pigment in the sample, and the rest is transmitted to the detector for a readout. Using the spectrophotometer, the student found the λ_max (the wavelength of light in nanometers (nm) that the pigment absorbs most intensely, for each sample) and recorded the results in Table 1. Table 1 also shows the transmittance and absorbance values at λ_max. Transmittance, T, is defined as the fraction of light, expressed as a decimal, which passes through the sample. Absorbance, A, is given by:

                                    A = –log(T)   or  10^–A = T

Experiment 2:

A student is given a leaf from an unknown source. She crushes and extracts the pigment according to the procedure in Experiment 1. Measuring the absorbance spectrum in the spectrophotometer produces the following readout, shown in Diagram 2.

                                                Diagram 2

In Experiment 2, at which of the following wavelengths, in nanometers, is the most amount of light transmitted through the sample?