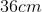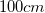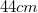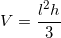Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Solid Geometry

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Volume Of A Figure

Chemicals to clean a swimming pool cost $0.24 per cubic foot of water. If a pool is 6 feet deep, 14 feet long and 8 feet wide, how much does it cost to clean the pool? Round to the nearest dollar.

Possible Answers:

$\$150$

$\$161$

$\$202$

$\$672$

$\$184$

Correct answer:

$\$161$

Explanation:

The volume of the pool can be determined by multiplying the length, width, and height together.

$V = 6 \times 8 \times 14 = 672 ft^{3}$

Each cubit foot costs 24 cents, so:

$672ft^3\times \$0.24=\$161.28\approx \$161$

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

A cube has edges that are three times as long as those of a smaller cube. The volume of the bigger cube is how many times larger than that of the smaller cube?

Possible Answers:

Correct answer:

Explanation:

If we let represent the length of an edge on the smaller cube, its volume is $x^{3}$ .

The larger cube has edges three times as long, so the length can be represented as . The volume is $(3x)^{3}$ , which is $27x^{3}$ .

The large cube's volume of $27x^{3}$ is 27 times as large as the small cube's volume of $x^{3}$ .

Report an Error

Example Question #41 : Cubes

A tank measuring 3in wide by 5in deep is 10in tall. If there are two cubes with 2in sides in the tank, how much water is needed to fill it?

Possible Answers:

134 in^3

150 in^3

16 in^3

8 in^3

160 in^3

Correct answer:

134 in^3

Explanation:

$Volume_{Tank} = Width \cdot Depth \cdot Height$

$Volume_{Tank} = 3in \cdot 5in \cdot 10in = 150 in^3$

$Volume_{Cube} = (Side)^3 = (2in)^3 = 8 in^3$

$Volume_{Water}=Volume_{Tank}-2(Volume_{Cube})$

$Volume_{Water}=150-2(8)$

$Voume_{Water}=150-16$

$Volume_{Water}=134in^3$

Report an Error

Example Question #3 : How To Find The Volume Of A Cube

What is the volume of a cube that has a side length of inches?

Possible Answers:

63in^3

343in^2

21in^3

49in^2

343 in^3

Correct answer:

343 in^3

Explanation:

We are given the side length of a cube so we simply plug that into the formula for the volume of a cube.

That formula is V =s^3 , and so the correct answer is

V=7^3=343in^3 .

Make sure to check your units, 343in^2 is the correct number, but the units are squared rather than cubed.

Report an Error

Example Question #3 : How To Find The Volume Of A Cube

What is the volume of a cube with a side of length 1 cm?

Possible Answers:

6cm^3

1cm

3cm^3

0cm^3

1cm^3

Correct answer:

1cm^3

Explanation:

The formula for the volume of a cube with a side of length is:
$\\V = s^3 \\V= 1^3 \\V= 1cm^3$

Report an Error

Example Question #8 : How To Find The Volume Of A Cube

A cube of sponge has volume 1000 cm^3 . When water is added, the sponge triples in length along each dimension. What is the new volume of the cube, in cubic centimeters?

Possible Answers:

2700cm^3

9000cm^3

30000cm^3

27000 cm^3

3000cm^3

Correct answer:

27000 cm^3

Explanation:

If our original cube has a volume of 1000cm^3 , then the length of one of its edges is $\sqrt[3]{1000} = 10cm$ . Triple each edge to 30cm , then cube the result, and we obtain 30^3 = 27000cm^3

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

Find the volume of a cube with side length 10.

Possible Answers:

$10\sqrt{2}$

1000

100

600

Correct answer:

1000

Explanation:

To find volume, simply cube the side length. Thus,

V=s^3=10^3=1000

Report an Error

Example Question #41 : Solid Geometry

Find the volume of a cube whose side length is 0.1.

Possible Answers:

0.1

0.001

0.01

Correct answer:

0.001

Explanation:

To solve, simply use the formula for volume of a cube. The volume of a cube is length times width times height. Since the height, width, and length are equal on a cube the formula becomes side cubed.

We are given the side length of 0.1 thus,

V=s^3=(0.1)^3=0.001

Report an Error

Example Question #42 : Solid Geometry

Find the volume of a cube given side length is .

Possible Answers:

1000

100

Correct answer:

1000

Explanation:

To solve, simply cube the side length. Thus,

V=s^3=10*10*10=1000

Report an Error

Example Question #1 : Pyramids

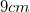
A square pyramid has a volume of 363cm^3 and a height of $\small 9cm$ . What is the perimeter of the base of the pyramid?

Possible Answers:

36cm

44cm

80cm

100cm

121cm

Correct answer:

44cm

Explanation:

The formula for the volume of a pyramid is:

$\small V=\frac{lwh}{3}$

We know that V=363 and h=9 ; however, this still leaves us with two variables in the equation: and . By definition, a square pyramid's base has sides of equal length, meaning that and are the same. Therefore, we can substitute $\small lw$ for $\small l\cdot l$ , or $\small l^2$ .

This gives us a new equation of:

$\small V=\frac{l^2h}{3}$

We then plug in the variables we know:

$\small 363=\frac{9l^2}{3}$

Multiply both sides by 3:

$\small 1089=9l^2$

Divide both sides by 9:

l^2=121

l=11

Therefore, we now know that the length of the pyramid's base is $\small 11cm$ . The question, however, asks for the perimeter of the pyramid's base. Since all of the sides of the base are the same, they must all be $\small 11cm$ . So we multiply $11cm\cdot 4=44cm$ . Therefore, the perimeter of the pyramid's base is $\small 44cm$ .

Report an Error

View ACT Math Tutors

Andrew
Certified Tutor

University of Wisconsin-Stevens Point, Bachelor of Science, Mathematics. University of Wisconsin-Oshkosh, Master of Science, ...

View ACT Math Tutors

Joseph
Certified Tutor

Florida Atlantic University, Bachelor of Science, Accounting.

View ACT Math Tutors

Shaftab
Certified Tutor

University of Engineering and Technology, Lahore, Pakistan, Bachelor of Engineering, Electrical Engineering. Quaid-i-Azam Uni...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Denver, Spanish Courses & Classes in Phoenix, MCAT Courses & Classes in Chicago, SAT Courses & Classes in Miami, LSAT Courses & Classes in New York City, ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Houston, ISEE Courses & Classes in Seattle, SSAT Courses & Classes in Seattle, ACT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in Boston, ACT Test Prep in San Francisco-Bay Area, GRE Test Prep in Atlanta, ACT Test Prep in Dallas Fort Worth, MCAT Test Prep in San Diego, SSAT Test Prep in San Diego, GRE Test Prep in New York City, MCAT Test Prep in Philadelphia, SAT Test Prep in Houston, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Solid Geometry

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #2 : How To Find The Volume Of A Figure

Example Question #1 : How To Find The Volume Of A Cube

Example Question #41 : Cubes

Example Question #3 : How To Find The Volume Of A Cube

Example Question #3 : How To Find The Volume Of A Cube

Example Question #8 : How To Find The Volume Of A Cube

Example Question #1 : How To Find The Volume Of A Cube

Example Question #41 : Solid Geometry

Example Question #42 : Solid Geometry

Example Question #1 : Pyramids

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: