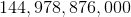ACT Math : Integers
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #11 : Permutation / Combination
A student is taking a test consisting of six questions. It is a multiple choice test and each question has four answers labelled A, B, C, and D. How many ways can the student answer all six questions if he does not choose the same answer for any two consecutive questions?
30
625
324
972
100
972
the student has four choices for the first question, but only three choices for each of the remaining questions since he does not choose answers with the same letter twice in a row. From the multiplicative counting principle, there are 4 × 3 × 3 × 3 × 3 x 3 = 972 ways Steve can answer the six questions.
Example Question #11 : Permutation / Combination
Ashley is modeling a new mix-and-match clothing line. Her stylist has selected 5 tops, 3 skirts, and 4 jackets for her photo shoot. Assuming that an outfit consists of one top, one skirt, and one jacket, how many outfits can Ashley create for the photo shoot?
20
12
45
30
60
60
In order to calculate the total possible number of combinations, we must multiply the number of possibilities for each piece by one another.
Example Question #11 : Permutation / Combination
In how many ways can the seven members of a students’ council pose in a line for a yearbook photograph if the chair and vice-chair must be side by side?
First find the number of arrangements in which the chair and vice-chair are together. Consider the chair and vice-chair as a unit. This pair as one unit can be arranged with the remaining five members in 
Therefore, there is a total of 2 * 720 = 1440 ways in which the chair and vice-chair are together.
Example Question #12 : Permutation / Combination
Sally is putting on jewelry and has decided to wear one necklace, one pair of earrings, and one ring. Her jewelry collection is listed below. How many different combinations of jewelry can she wear?
|
Necklace |
Earrings |
Ring |
|
short |
studs |
gold |
|
long |
hoops |
silver |
|
|
dangling |
|
18
3
36
12
7
12
To find the number of different combinations, we must use the fundamental counting principal to multiply the number of options in each category together:
(2)(3)(2) = 12
Example Question #1 : How To Find Permutation Notation
In permutation notation, what does 8P4 represent?
336
1680
6720
210
1680
The expression 8P4 represents the number of permutations of 8 objects arranged 4 at a time. Thus, 8 x 7 x 6 x 5 = 1680
Example Question #11 : Permutation / Combination
How many different ways can five books be lined up on a shelf?
80
150
100
60
120
120
Order matters, so we use permutations: (5)(4)(3)(2)(1) = 120
There are five possibilities for the first book, four possibilities for the second book, three for the third, and two for the fourth, and one possibility for the last book.
Example Question #1721 : Act Math
How many different ways can cheese slices be stacked in piles containing 
Since the order matters, you are dealing with a permutation in this question. A permutation like this could be done with the equation:
For our values, this would be:
However, it is easiest just to think of this like it has 
more easily.
This is 
Example Question #651 : Arithmetic
A car averages 29 miles per gallon. If gas costs $3.75 per gallon how much money would need to be spent on gas to travel 1464.5 miles?
$108.75
$5491.88
$189.38
$50.5
None of the other answers
$189.38
The question is asking for the amount of money that would need to be spent on gas. Using the value given for the miles per gallon of the car and the amount of miles traveled it is possible to determine the gallons of fuel that will be required. This will be set up as 1464.5 miles travelled divided by the 29 miles per gallon that the car gets. This leaves us with 50.5 gallons of fuel used. From this point we can multiply the amount of fuel used, 50.5 gallons, by the price of fuel per gallon, $3.75, to obtain the amount of money that will spent on fuel, $189.38.
Example Question #141 : Integers
Connie's car gets 35 miles per gallon of gas. How much gas will she need to take a 525 mile trip? Round to the nearest gallon.
20
25
23
17
15
15
This becomes a division problem: 525 miles ÷ 35 miles per gallon = 15 gallons
Example Question #1724 : Act Math
A father buys a bag of marbles. He divides the marbles among his 5 children, who receive 24 marbles each. If there had been 6 children, how many marbles would each one get?
18
22
20
24
20
There were a total of 120 marbles to begin with, since 5 * 24 = 120.
If the marbles are split between 6 children, then each child gets 120/6 = 20 marbles each.
All ACT Math Resources
