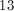We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1201 : Algebra

Alice is twice as old as Tom, but four years ago, she was three years older than Tom is now. How old is Tom now?

Possible Answers:

$\dpi{100} \small 13$

$\dpi{100} \small 3$

$\dpi{100} \small 7$

$\dpi{100} \small 9$

$\dpi{100} \small 21$

Correct answer:

$\dpi{100} \small 7$

Explanation:

The qustion can be broken into two equations with two unknows, Alice age $\dpi{100} \small (A)$ and Tom's age $\dpi{100} \small (T)$ .

$\dpi{100} \small A=2T$

$\dpi{100} \small A-4=T+3$

$\dpi{100} \small 2T-4=T+3$

$\dpi{100} \small T=7$

Report an Error

Example Question #1202 : Algebra

A jet goes from City 1 to City 2 at an average speed of 600 miles per hour, and returns along the same path at an average speed if 300 miles per hour. What is the average speed, in miles per hour, for the trip?

Possible Answers:

400miles/hour

350miles/hour

500miles/hour

300miles/hour

450miles/hour

Correct answer:

400miles/hour

Explanation:

Chose a number for the distance between City 1 and 2; 1800 works well, as it is a multiple of 600 and 300.

Now, find the time for each trip, the total distance, and the total time.

$t_1=\frac{d_1}{v_1}=\frac{1800}{600}=3$

$t_2=\frac{d_2}{v_2}=\frac{1800}{300}=6$

$total\ t=t_1+t_2=3+6=9$

$total\ d=d_1+d_2=1800+1800=3600$

Now we can find the average speed by dividing the total distance by the total time.

$average speed = \frac{total distance}{total time} = \frac{3600 miles}{9 hours} = 400 miles/hour$

Report an Error

Example Question #1203 : Algebra

$f(x)=3x^{2}-5$

g(x)=9-2x

Find f(g(5)) .

Possible Answers:

131

Correct answer:

Explanation:

Plug 5 into g(x) first:

g(5)=9-2(5)

=-1

Now, plug this answer into f(x) :

$f(-1)=3(-1)^{2}-5$

=3-5

=-2

Report an Error

Example Question #1204 : Algebra

If f(x) = 3x + 7 and g(x) = x^2 - 12 , what is f(g(x)) ?

Possible Answers:

9x^2 - 29

3x^2 - 29

3x^2 + 29

9x^3 + 29

3x^3 - 29

Correct answer:

3x^2 - 29

Explanation:

Plug g(x) into f(x) as if it is just a variable. This gives f(g(x)) = 3(x²– 12) + 7.

Distribute the 3: 3x²– 36 + 7 = 3x²– 29

Report an Error

Example Question #31 : How To Find F(X)

If h(x)=2x+3 and g(x) = x-4 , then g(h(3))=?

Possible Answers:

Correct answer:

Explanation:

To answer this question, we need to understand exactly what g(h(3)) actually means.

We start from the inside of the parentheses and work outwards. Therefore, we first solve for h(3) using the equation for h(x) provided for us. So, for this data:

h(3)=h(x)=2x+3= 2(3)+3=6+3=9

Therefore, h(3)=9 . We now take that answer and plug it in for the value within g(x) = x-4 . So, for this data:

g(x) = x-4=9-4=5

Therefore, the answer to g(h(3)) is .

Report an Error

Example Question #47 : Algebraic Functions

If f(x) = 2x^2 + 3x + 2 , what does f(x + 4) equal?

Possible Answers:

2x^2 + 11x + 30

2x^2 + 19x + 46

2x^2 + 12x + 56

2x^2 + 10x + 42

2x^2 + 19x + 38

Correct answer:

2x^2 + 19x + 46

Explanation:

For a question like this, treat it just like you would the use of a numeric value for evaluating your function. All you do is “plug in” x + 4 . Thus, for this function, you get:

f(x + 4) = 2(x + 4)^2 + 3(x+4) + 2

Next, you just need to distribute everything correctly:

f(x + 4) = 2(x + 4)(x + 4) + 3x+12 + 2

f(x + 4) = 2(x^2 + 8x + 16) + 3x + 14

f(x + 4) = 2x^2 + 16x + 32 + 3x + 14

f(x + 4) = 2x^2 + 19x + 46

Report an Error

Example Question #1205 : Algebra

If f(x) = 3x + 20 , what is f(4x^2 + 5x) ?

Possible Answers:

12x^2 + 5x + 20

12x^2 + 25x

47x^3

12x^2 + 15x + 20

4x^2 + 8x + 20

Correct answer:

12x^2 + 15x + 20

Explanation:

For a question like this, treat it just like you would the use of a numeric value for evaluating your function. All you do is “plug in” 4x^2 + 5x . Thus, for this function, you get:

f(4x^2 + 5x) = 3(4x^2 + 5x) + 20

From here, you merely need to distribute correctly!

f(4x^2 + 5x) = 12x^2 + 15x + 20

Report an Error

Example Question #52 : Algebraic Functions

When written in symbols, “The square of the sum of and equals 100 ” is represented as:

Possible Answers:

m^2 + n^2 = 100

m^2 + n = 100

m + n = 100

(m + n)^2 = 100

m + n^2 = 100

Correct answer:

(m + n)^2 = 100

Explanation:

“The square of the sum” means that the summation of the terms is done first, and that summation is squared, which corresponds to the term (m+n)^2 .

Report an Error

Example Question #53 : Algebraic Functions

Given the functions f(x)=2x+4 and g(x)=4x , what is f(g(x)) when x=2 ?

Possible Answers:

Correct answer:

Explanation:

In order to find f(g(x)) , work from the inside out. In other words, begin by finding g(x) , or g(2) since x=2.

g(2)=4(2)=8

Now, seeing as g(x)=8, f(g(x))=f(8) . Substitute for in f(x) in order to find the answer.

f(8)=2(8)+4=20

f(g(x))=20

Report an Error

Example Question #52 : Algebraic Functions

Find f(g(x)) when f(x)=x^2 , g(x)=2x-4 , and x=3 .

Possible Answers:

Correct answer:

Explanation:

Start on the inside by finding g(x) when x=3 .

g(3)=2(3)-4=2

Now that we know g(x)=2 , we can substitute g(x) for in f(g(x)) .

Find f(2) .

$f(2)=2^{2}=4$

Report an Error

View ACT Math Tutors

Sarah
Certified Tutor

View ACT Math Tutors

Philip
Certified Tutor

Northern Virginia Community College, Associate in Science, Computer Science. George Mason University, Bachelor of Science, Co...

View ACT Math Tutors

Barry
Certified Tutor

State University of New York at Binghamton, Master of Science, Economics.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Boston, GRE Courses & Classes in Los Angeles, GMAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Miami, ACT Courses & Classes in New York City, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in Denver, SAT Courses & Classes in Seattle, SAT Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in Miami, SAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Washington DC, GMAT Test Prep in Atlanta, MCAT Test Prep in Denver, ACT Test Prep in San Diego, GRE Test Prep in New York City, SSAT Test Prep in Atlanta, GRE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1201 : Algebra

Example Question #1202 : Algebra

Example Question #1203 : Algebra

Example Question #1204 : Algebra

Example Question #31 : How To Find F(X)

Example Question #47 : Algebraic Functions

Example Question #1205 : Algebra

Example Question #52 : Algebraic Functions

Example Question #53 : Algebraic Functions

Example Question #52 : Algebraic Functions

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: