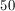Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Solve for $\displaystyle x$:

$\frac{x+1}{4}-\frac{x}{3}=6$ $\displaystyle \frac{x+1}{4}-\frac{x}{3}=6$

Possible Answers:

x=-69 $\displaystyle x=-69$

x=26 $\displaystyle x=26$

x=42 $\displaystyle x=42$

x=-72 $\displaystyle x=-72$

x=60 $\displaystyle x=60$

Correct answer:

x=-69 $\displaystyle x=-69$

Explanation:

Solve for x:

$\frac{x+1}{4}-\frac{x}{3}=6$ $\displaystyle \frac{x+1}{4}-\frac{x}{3}=6$

Step 1: Find the least common denominator, $\displaystyle 12$, and adjust the fractions accordingly:

$\left (\frac{3}{3} \right )\cdot \left ( \frac{x+1}{4} \right ) - \left ( \frac{4}{4} \right )\cdot \left ( \frac{x}{3} \right )=6$ $\displaystyle \left (\frac{3}{3} \right )\cdot \left ( \frac{x+1}{4} \right ) - \left ( \frac{4}{4} \right )\cdot \left ( \frac{x}{3} \right )=6$

$\left ( \frac{3x+3}{12} \right )-\left ( \frac{4x}{12} \right )=6$ $\displaystyle \left ( \frac{3x+3}{12} \right )-\left ( \frac{4x}{12} \right )=6$

Solve for $\displaystyle x$:

$\frac{3x+3-4x}{12}=6$ $\displaystyle \frac{3x+3-4x}{12}=6$

$\displaystyle 3x+3-4x=72$

-x=69 $\displaystyle -x=69$

x=-69 $\displaystyle x=-69$

Report an Error

Example Question #65 : Algebraic Fractions

If $\frac{6}{x}=\frac{9}{19}$ $\displaystyle \frac{6}{x}=\frac{9}{19}$ , then what is the value of $\displaystyle x$?

Possible Answers:

38/3

none of these

9/114

7/12

3/38

Correct answer:

38/3

Explanation:

cross multiply:

(6)(19) = 9x

114=9x

x = 38/3

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

$\dpi{100} \small \frac{4 }{x} = \frac{2}{25}$ $\displaystyle \dpi{100} \small \frac{4 }{x} = \frac{2}{25}$

Find x.

Possible Answers:

$\dpi{100} \small 50$ $\displaystyle \dpi{100} \small 50$

$\dpi{100} \small 0.25$ $\displaystyle \dpi{100} \small 0.25$

None

$\dpi{100} \small \frac{8}{25}$ $\displaystyle \dpi{100} \small \frac{8}{25}$

$\dpi{100} \small \frac{25}{8}$ $\displaystyle \dpi{100} \small \frac{25}{8}$

Correct answer:

$\dpi{100} \small 50$ $\displaystyle \dpi{100} \small 50$

Explanation:

Cross multiply:

$\dpi{100} \small 4 \times 25 = 2x$ $\displaystyle \dpi{100} \small 4 \times 25 = 2x$

$\dpi{100} \small 100 = 2x$ $\displaystyle \dpi{100} \small 100 = 2x$

$\dpi{100} \small x = 50$ $\displaystyle \dpi{100} \small x = 50$

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.

Possible Answers:

$\frac{1}{3}$ $\displaystyle \frac{1}{3}$

$\displaystyle 12$

$\displaystyle 6$

$\displaystyle 18$

$\frac{1}{2}$ $\displaystyle \frac{1}{2}$

Correct answer:

$\displaystyle 6$

Explanation:

Let numerator = N and denominator = D.

According to the first statement,

N = (D x 5) + 4.

According to the second statement, N / 2 = 3 * D.

Let's multiply the second equation by –2 and add itthe first equation:

–N = –6D

+[N = (D x 5) + 4]

–6D + (D x 5) + 4 = 0

–1D + 4 = 0

D = 4

Thus, N = 24.

Therefore, N/D = 24/4 = 6.

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Solve the following equation for the given variable:

$\frac{2}{3x}=4$ $\displaystyle \frac{2}{3x}=4$

Possible Answers:

$x = \frac{3}{4}$ $\displaystyle x = \frac{3}{4}$

$x = \frac{8}{3}$ $\displaystyle x = \frac{8}{3}$

$x = \frac{1}{5}$ $\displaystyle x = \frac{1}{5}$

$x = \frac{1}{6}$ $\displaystyle x = \frac{1}{6}$

$x = \frac{3}{2}$ $\displaystyle x = \frac{3}{2}$

Correct answer:

$x = \frac{1}{6}$ $\displaystyle x = \frac{1}{6}$

Explanation:

To solve this equation we have to multiply both sides by the denominator to get rid of the fraction.

Doing this yields

2 = 12x $\displaystyle 2 = 12x$

Then to solve the last step is to isolate the variable by dividing both sides by 12.
Thus,

$x = \frac{2}{12}=\frac{1}{6}$ $\displaystyle x = \frac{2}{12}=\frac{1}{6}$.

Report an Error

Example Question #5 : How To Solve For A Variable As Part Of A Fraction

For what value of $\displaystyle x$ is the equation $\frac{4}{12}=\frac{5}{x}$ $\displaystyle \frac{4}{12}=\frac{5}{x}$ true?

Possible Answers:

$\displaystyle 6$

$\displaystyle 14$

$\displaystyle 3$

$\displaystyle 12$

$\displaystyle 15$

Correct answer:

$\displaystyle 15$

Explanation:

When the equation is cross multiplied, it becomes

$\\ 4\cdot x=5\cdot 12 \\4x = 60$ $\displaystyle \\ 4\cdot x=5\cdot 12 \\4x = 60$.

Hence,

$x =\frac{60}{4}$ $\displaystyle x =\frac{60}{4}$, or x=15 $\displaystyle x=15$.

Report an Error

Example Question #4 : How To Solve For A Variable As Part Of A Fraction

Solve the following equation for $\displaystyle x$:

$\frac{36}{5x} = 4$ $\displaystyle \frac{36}{5x} = 4$.

Reduce any fractions in your final answer.

Possible Answers:

x = 5 $\displaystyle x = 5$

$x = \frac{5}{9}$ $\displaystyle x = \frac{5}{9}$

x = 3 $\displaystyle x = 3$

$x = \frac{9}{5}$ $\displaystyle x = \frac{9}{5}$

$x = \frac{36}{20}$ $\displaystyle x = \frac{36}{20}$

Correct answer:

$x = \frac{9}{5}$ $\displaystyle x = \frac{9}{5}$

Explanation:

To solve an equation with a variable in a fraciton, treat the denominator as a constant value and multiply both sides of the equation by the denominator in order to eliminate it.
$\\5x * \left(\frac{36}{5x}\right) = 4 * 5x\\ \newline 36 = 20x \newline \newline \frac{36}{20} = x \\ \newline \frac{9}{5}= x$ $\displaystyle \\5x * \left(\frac{36}{5x}\right) = 4 * 5x\\ \newline 36 = 20x \newline \newline \frac{36}{20} = x \\ \newline \frac{9}{5}= x$

Report an Error

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Solve for $\displaystyle x$: $\frac{x}{12}=3$ $\displaystyle \frac{x}{12}=3$

Possible Answers:

$\displaystyle 4$

$\frac{1}{36}$ $\displaystyle \frac{1}{36}$

$\frac{1}{3}$ $\displaystyle \frac{1}{3}$

$\displaystyle 24$

$\displaystyle 36$

Correct answer:

$\displaystyle 36$

Explanation:

To find the answer, multiply the right side by $\displaystyle 12$. The result is 36=x $\displaystyle 36=x$.

Report an Error

Example Question #61 : Algebraic Fractions

Solve for $\displaystyle x$:

$\frac{3}{4}=\frac{5x+10}{20}$ $\displaystyle \frac{3}{4}=\frac{5x+10}{20}$

Possible Answers:

$\displaystyle 1$

$\displaystyle 4$

$\displaystyle 5$

$\displaystyle 2$

$\displaystyle 3$

Correct answer:

$\displaystyle 1$

Explanation:

To solve this problem you must cross mutiply, then set the two equations equal to each other. Your first equation is $3\left ( 20\right )$ $\displaystyle 3\left ( 20\right )$, your second is $4\left ( 5x+10\right )=20+40$ $\displaystyle 4\left ( 5x+10\right )=20+40$. This gives you $\displaystyle 60=20x+40$. Subtract $\displaystyle 40$ from both sides, so you have 20=20x $\displaystyle 20=20x$, divide by $\displaystyle 20$ on both sides and you have x=1 $\displaystyle x=1$.

Report an Error

Example Question #11 : How To Solve For A Variable As Part Of A Fraction

Solve for $\displaystyle x$:

$\frac{14}{x+3}=\frac{2}{3}$ $\displaystyle \frac{14}{x+3}=\frac{2}{3}$

Possible Answers:

19.5 $\displaystyle 19.5$

$\displaystyle 18$

$\displaystyle 20$

$\displaystyle 16$

Correct answer:

$\displaystyle 18$

Explanation:

Cross multiply: $\displaystyle 42=2(x+3)$

Distribute: 42=2x+6 $\displaystyle 42=2x+6$

Solve for $\displaystyle x$: 36=2x $\displaystyle 36=2x$

18=x $\displaystyle 18=x$

Report an Error

View ACT Math Tutors

Foysal
Certified Tutor

Towson University, Bachelor, Physics . Virginia Commonwealth University, Master of Science, Health Physics.

View ACT Math Tutors

Janani
Certified Tutor

University of Central Florida, Bachelor of Science, Health Sciences, General.

View ACT Math Tutors

David
Certified Tutor

Hope College, Bachelor of Science, Economics.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Miami, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in Chicago, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in New York City, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Boston, Spanish Courses & Classes in Miami, ACT Courses & Classes in Phoenix, SSAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Houston, GRE Test Prep in San Francisco-Bay Area, LSAT Test Prep in Denver, LSAT Test Prep in Washington DC, MCAT Test Prep in Chicago, ACT Test Prep in Phoenix, GMAT Test Prep in Philadelphia, SAT Test Prep in Philadelphia, MCAT Test Prep in Atlanta, MCAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #2 : How To Solve For A Variable As Part Of A Fraction

Example Question #65 : Algebraic Fractions

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #5 : How To Solve For A Variable As Part Of A Fraction

Example Question #4 : How To Solve For A Variable As Part Of A Fraction

Example Question #1 : How To Solve For A Variable As Part Of A Fraction

Example Question #61 : Algebraic Fractions

Example Question #11 : How To Solve For A Variable As Part Of A Fraction

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: