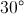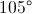All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : Acute / Obtuse Triangles
If the vertex angle of an isosceles triangle is 30 degrees, what is the value of the angle that is exterior to one of the base angles?
First, you subtract one angle so 

Example Question #1 : How To Find The Perimeter Of An Acute / Obtuse Triangle
The side lengths of a triangle are 
To find the perimeter of a triangle, add up its side lengths.
Example Question #2 : How To Find The Perimeter Of An Acute / Obtuse Triangle
The side lengths of a triangle, in inches, are 
Find the perimeter of a triangle by adding up all its sides.
Example Question #3 : How To Find The Perimeter Of An Acute / Obtuse Triangle
A triangle has side lengths 


To find the perimeter of a triangle, add up all the side lengths.
Example Question #4 : How To Find The Perimeter Of An Acute / Obtuse Triangle
In terms of 

To find the perimeter of a triangle, add up all of its sides.
Example Question #5 : How To Find The Perimeter Of An Acute / Obtuse Triangle
In terms of 

To find the perimeter of a triangle, add up all of its sides.
Example Question #6 : How To Find The Perimeter Of An Acute / Obtuse Triangle
In terms of 

To find the perimeter of a triangle, add up all of its sides.
Example Question #7 : How To Find The Perimeter Of An Acute / Obtuse Triangle
In terms of 

To find the perimeter of a triangle, add up all of its sides.
Example Question #8 : How To Find The Perimeter Of An Acute / Obtuse Triangle
Find the perimeter of a triangle with side lengths 
To find the perimeter of a triangle, add up all of its sides.
Example Question #9 : How To Find The Perimeter Of An Acute / Obtuse Triangle
Bill has a triangular garden that he needs to fence. The garden has side lengths of 
To find how much fencing Bill needs, you will need to find the perimeter of the triangle. The perimeter of a triangle is found by adding up all the sides together.
All SSAT Upper Level Math Resources