All SSAT Upper Level Math Resources
Example Questions
Example Question #7 : Use Similar Triangles To Show Equal Slopes: Ccss.Math.Content.8.Ee.B.6
Give the 


The line has no 
First, find the slope of the line, using the slope formula
setting 
By the point-slope formula, this line has the equation
where

or
To find the 


The 

Example Question #132 : Grade 8
Give the 


First, find the slope of the line, using the slope formula
setting 
By the point-slope formula, this line has the equation
where

or
To find the 


The 

Example Question #272 : Geometry
Give the 


By the point-slope formula, this line has the equation
where
By substitution, the equation becomes

To find the 


The 

Example Question #131 : Grade 8
Find the y-intercept:
Rewrite the equation in slope-intercept form, 
The y-intercept is 

Example Question #271 : Geometry
What is the 
The graph has no 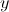
The 




The 

Example Question #12 : How To Find X Or Y Intercept
Define a function 


The 





The correct choice is 
Example Question #13 : How To Find X Or Y Intercept
Define a function 


(a)
(b)
Both (a) and (b)
(a), but not (b)
(b), but not (a)
Neither (a) nor (b)
Neither (a) nor (b)
An 






We can most easily determine whether 






Similarly, substituting 3 for 



Example Question #15 : How To Find X Or Y Intercept
Define 




An 






Substituting the definition, we get
Solving for 
The 


To determine which of the four choices is correct, substitute 





The correct choice is 
Example Question #1 : How To Find The Equation Of A Curve
If the 


Write the slope-intercept form.
The point given the x-intercept of 6 is 
Substitute the point and the slope into the equation and solve for the y-intercept.
Substitute the y-intercept back to the slope-intercept form to get your equation.
Example Question #2 : How To Find The Equation Of A Curve
A vertical parabola on the coordinate plane has vertex 


Give its equation.
Insufficient information is given to determine the equation.
The equation of a vertical parabola, in vertex form, is

where 

To find 


The equation, in vertex form, is 
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources






















































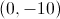


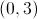









































![y = a[x-(-4)]^{2}+10](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/349648/gif.latex)













