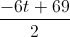All SSAT Upper Level Math Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Hexagon
A regular hexagon has perimeter 9 meters. Give the length of one side in millimeters.
One meter is equal to 1,000 millimeters, so the perimeter of 9 meters can be expressed as:
9 meters = 
Since the six sides of a regular hexagon are congruent, divide by 6:

Example Question #1 : Areas And Perimeters Of Polygons
A hexagon with perimeter 60 has four congruent sides of length 

The perimeter of a polygon is the sum of the lengths of its sides. Let:

Now we can set up an equation and solve it for 

Example Question #2 : Perimeter Of Polygons
Two sides of a hexagon have a length of 


The perimeter of a polygon is the sum of the lengths of its sides. So we can write:
Example Question #2 : How To Find The Perimeter Of A Hexagon
A regular hexagon has perimeter 15 feet. Give the length of one side in inches.
As the six sides of a regular hexagon are congruent, we can write:


One feet is equal to 12 inches, so we can write:

Example Question #1 : Perimeter Of Polygons
Each interior angle of a hexagon is 120 degrees and the perimeter of the hexagon is 120 inches. Find the length of each side of the hexagon.
Since each interior angle of a hexagon is 120 degrees, we have a regular hexagon with identical side lengths. And we know that the perimeter of a polygon is the sum of the lengths of its sides. So we can write:

Example Question #3 : Perimeter Of Polygons
A hexagon with perimeter of 48 has three congruent sides of 


The perimeter of a polygon is the sum of the lengths of its sides. Since three sides are congruent with the length of 

Now we should solve the equation for 
Example Question #3 : How To Find The Perimeter Of A Hexagon
A regular pentagon has sidelength one foot; a regular hexagon has sidelength ten inches. The perimeter of a regular octagon is the sum of the perimeters of the pentagon and the hexagon. What is the measure of one side of the octagon?
A regular polygon has all of its sides the same length. The pentagon has perimeter 



Example Question #1 : Areas And Perimeters Of Polygons
Find the perimeter of a hexagon with a side length of 
A hexagon has six sides. The perimeter of a hexagon is:
Substitute the side length.
Example Question #1 : How To Find The Perimeter Of A Pentagon
A pentagon with perimeter 54 has three congruent sides of length 

The perimeter of a polygon is the sum of the lengths of its sides. If we let 

Example Question #761 : Geometry
A regular pentagon has perimeter 7 meters. Give the length of one side in millimeters.
One meter is equal to 1,000 millimeters, so the perimeter of 7 meters can be expressed as:
7 meters = 
Since the five sides of a regular pentagon are congruent, divide by 5:

Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources





















![Perimeter=2\left [ t+(t+1)+(t-1) \right ]=2(3t)=6t](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/111948/gif.latex)