Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Elementary Level Math : Plane Geometry

Study concepts, example questions & explanations for SSAT Elementary Level Math

Create An Account

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Triangles

What is the area of a triangle with a base of 11 and a height of 4?

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a triangle is $\frac{base \cdot height}{2}$ . First, we should multiply 11 (base) x 4 (height), to get a total of 44. Next, we need to divide 44 by 2, which gives us a total area of 22.

Report an Error

Example Question #2 : Triangles

You can find the area of a triangle if you know ___________.

Possible Answers:

its angles

two side lengths

the height and base

the perimeter

Correct answer:

the height and base

Explanation:

$Area _{\Delta } = \frac{1}{2}\times base \times height$

Report an Error

Example Question #5751 : Ssat Elementary Level Quantitative (Math)

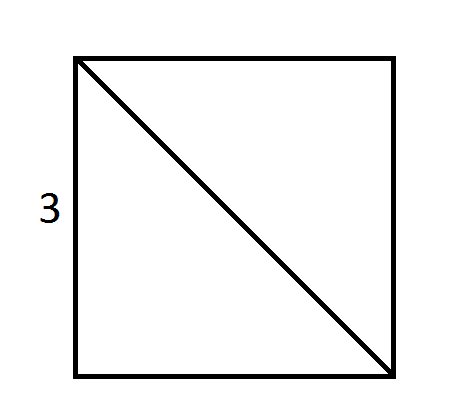
Squareslice

The square shown above has a side length of 3 and is divided into two triangles by its diagonal. What is the area of one of the triangles?

Possible Answers:

4.5

6.5

12.25

Correct answer:

4.5

Explanation:

The area of the square is side times side, $3\times3=9$ .

Each triangle is half of the square, $9\div2=4.5$ .

Report an Error

Example Question #5751 : Ssat Elementary Level Quantitative (Math)

Screen_shot_2014-01-10_at_1.07.49_pm

What is the area of the triangle?

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a triangle is

$\frac{base \times height}{2}$

First, we should multiply (base) $\times$ (height), to get a total of .

Next, we need to divide by , which gives us a total area of .

Report an Error

Example Question #5752 : Ssat Elementary Level Quantitative (Math)

An isosceles triangle has a base of 12 cm and a height of 6 cm. What is the area of the triangle?

Possible Answers:

$36\: cm^{2}$

$72\: cm^{2}$

$18\, cm^{2}$

$12\: cm^{2}$

Correct answer:

$36\: cm^{2}$

Explanation:

To find the area of a triangle, you must multiply $\frac{1}{2}$ by the base (12 cm) by the height (6 cm):

$\frac{12\: cm}{2}\times6 \: cm=36\: cm^{2}$

Therefore the area of this triangle is $36\: cm^{2}$ .

Report an Error

Example Question #6 : Triangles

A triangle has a base of 14 and a height of 8. What is the area of the triangle?

Possible Answers:

112

Correct answer:

Explanation:

To find the area of a triangle, multiply the base (14) by the height (8) and divide by 2:

$\frac{14}{2}\times8=56$

Therefore the area of this triangle is .

Report an Error

Example Question #7 : Triangles

Screen_shot_2014-01-06_at_12.34.19_pm

What is the area of the triangle?

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a triangle is $\frac{base \times height}{2}$ .

$A = \frac{6\times 8}{2}=24$

Report an Error

Example Question #5753 : Ssat Elementary Level Quantitative (Math)

If a triangle has a base of 3 inches and a height of 8 inches, what is the area of the triangle?

Possible Answers:

$16\;in^2$

$11\;in^2$

$32\;in^2$

$24\;in^2$

$12\;in^{2}$

Correct answer:

$12\;in^{2}$

Explanation:

The formula for the area of a triangle is $\frac{1}{2} \times base \times height= area$ .

Plug in the values given to solve the equation:

$\frac{1}{2}(3\;in)(8\;in)=$

$\frac{1}{2}\times 3\;in \times 8\;in = \frac{1}{2}\;\times24\;in^{2}=12\;in^2$

Report an Error

Example Question #5754 : Ssat Elementary Level Quantitative (Math)

A triangle has a base of 10 centimeters and a height of 12 centimeters. What is the area of the triangle?

Possible Answers:

$22\ cm^{2}$

$120\ cm^{2}$

$72\ cm^{2}$

$60\ cm^{2}$

$70\ cm^{2}$

Correct answer:

$60\ cm^{2}$

Explanation:

The formula for the area of a triangle is $area=\frac{1}{2}(base)(height)$ .

Plug in the given values to solve for the area:

$\frac{1}{2}\times10cm\times12cm$

= $5cm\times12cm$

= 60cm^2

The area of this triangle is $60cm^{2}$ .

Report an Error

Example Question #5754 : Ssat Elementary Level Quantitative (Math)

What is the area of a right triangle with a base of length 4 and a height that is 3 times longer than the base?

Possible Answers:

Correct answer:

Explanation:

The area of a triangle is given by the formula $A = \frac{1}{2}\times b \times h$ , where is the length of the base and is the height.

First let's figure out the height. The base is 4, and the height is 3 times greater than the base:

$3 \times 4 = 12$

Now plug the base and height into the area formula:

$A = 0.5 \times 4 \times 12 = 2 \times 12 = 24$

The area of the triangle is 24.

Report an Error

View SSAT- Elementary Level Tutors

Varun
Certified Tutor

University of Arizona, Bachelor of Science, Aerospace Engineering.

View SSAT- Elementary Level Tutors

Lorie
Certified Tutor

Appalachian State University, Doctorate (PhD), Educational Leadership - Instructional Tech.

View SSAT- Elementary Level Tutors

Candice
Certified Tutor

University of Chicago, Bachelor in Arts, English. The New School, Master of Fine Arts, Creative Writing.

All SSAT Elementary Level Math Resources

12 Diagnostic Tests 526 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Atlanta, ISEE Tutors in Boston, Chemistry Tutors in Dallas Fort Worth, English Tutors in Denver, Spanish Tutors in Atlanta, Physics Tutors in Atlanta, SAT Tutors in Chicago, LSAT Tutors in Seattle, Algebra Tutors in Washington DC, Computer Science Tutors in Phoenix

Popular Courses & Classes

GMAT Courses & Classes in Boston, ACT Courses & Classes in New York City, GMAT Courses & Classes in Miami, GRE Courses & Classes in Atlanta, SSAT Courses & Classes in Denver, MCAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, Spanish Courses & Classes in San Diego, MCAT Courses & Classes in San Diego, LSAT Courses & Classes in Washington DC

Popular Test Prep

ACT Test Prep in Seattle, GMAT Test Prep in Miami, GMAT Test Prep in Atlanta, GRE Test Prep in Atlanta, GMAT Test Prep in Los Angeles, LSAT Test Prep in Boston, SSAT Test Prep in Seattle, ACT Test Prep in Phoenix, LSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Elementary Level Math : Plane Geometry

Study concepts, example questions & explanations for SSAT Elementary Level Math

All SSAT Elementary Level Math Resources

Example Questions

Example Question #1 : Triangles

Example Question #2 : Triangles

Example Question #5751 : Ssat Elementary Level Quantitative (Math)

Example Question #5751 : Ssat Elementary Level Quantitative (Math)

Example Question #5752 : Ssat Elementary Level Quantitative (Math)

Example Question #6 : Triangles

Example Question #7 : Triangles

Example Question #5753 : Ssat Elementary Level Quantitative (Math)

Example Question #5754 : Ssat Elementary Level Quantitative (Math)

Example Question #5754 : Ssat Elementary Level Quantitative (Math)

All SSAT Elementary Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: