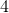SSAT Elementary Level Math : Plane Geometry
Study concepts, example questions & explanations for SSAT Elementary Level Math
All SSAT Elementary Level Math Resources
Example Questions
Example Question #6 : Lines
What is a line segment?
A line that has a start point but no end point.
A line that is always smaller than 10 centimeters.
A part of a line that connects two points.
A line that has no start or end points.
A line that is always greater than 10 centimeters.
A part of a line that connects two points.
A line segment is a part of a line that connects two points. It is different than a line and a ray because it has a defined start and end point.
Example Question #661 : Plane Geometry
Which statement is true regarding line segments?
A line segment has one endpoint, but continues indefinitely in one direction.
A line segment has three endpoints.
A line segment is a "piece" of a line and has two endpoints.
A line segment extends in both directions without endpoints.
A line segment is curved.
A line segment is a "piece" of a line and has two endpoints.
A line segment is a piece of a line connected by two endpoints.
Example Question #662 : Plane Geometry
A line is connected from 
Write the distance formula.
Substitute the points and solve for the distance.
Example Question #5821 : Ssat Elementary Level Quantitative (Math)
Find the length of a line which starts at the point (1,7) and goes till (9,7).
To solve, simply realize the distance between these points will just be the difference of their x values since their y values stay the same.
These points are on a horizontal line.
Thus,
Example Question #663 : Plane Geometry
Find the length of a line connecting the points (1,3) and (7,8).
To solve, simply use the distance formula. Thus,
It is important to remember that with the distance formula, you must keep the order of x2-x1 and y2-y1 consistent. It doesn't matter which point you choose to be 2 and which one you choose to be 1, but once you do, you must keep it in that order for both instances.
Example Question #664 : Geometry
On a line segment, there are two points. One is at 
When dealing with a number line, the distance of a point is measured in its distance from 
To get the total distance you just add the two distances together
Example Question #665 : Geometry
Find the length of the line shown below:
In order to find the length of the line, you have to find the difference between the points.
The first point is 4, and the second point is 21.
therefore the length of the line is 
Example Question #662 : Plane Geometry
Find the average of the two endpoints to find their midpoint. To find the average of two numbers, add them together and divide by two.
Example Question #663 : Plane Geometry
How many lines of symmetry does a square have?
A line of symmetry is the imaginary line that you draw through a shape so that you can fold the image over the line and have both halves match exactly. Any regular shape has as many lines of symmetry as it does sides. Since a square has four sides, the correct answer is 4!
Example Question #664 : Plane Geometry
How many lines of symmetry does an octagon have?
A line of symmetry divides a shape into two equal and identical halves. Any regular shape has as many lines of symmetry as it does sides. Since octagons have eight sides, the correct answer is 8.
Certified Tutor
All SSAT Elementary Level Math Resources
