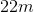SSAT Elementary Level Math : Plane Geometry
Study concepts, example questions & explanations for SSAT Elementary Level Math
All SSAT Elementary Level Math Resources
Example Questions
Example Question #511 : Rectangles
Find the perimeter of the rectangle.
A rectangle has a length of 12cm and a width of 4cm. What is the perimeter of this rectangle.
To find the perimeter of a rectangle, you must first understand that a rectangle's opposite sides are equal. Therefore if you know the length of one side it is the identical length of the opposite side.
32cm is your answer.
Example Question #512 : Rectangles
Find the perimeter of a rectangle.
A rectangle has a width of 7cm and a length of 10cm. What is the perimeter of the rectangle?
First you need to understand that opposite sides of a rectangle are equal. Then you are able to add the value of each side to itself and then add your sums together to get the perimeter of a rectangle.
Example Question #581 : Geometry
Use the following rectangle to answer the question:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, let's look at the rectangle.
We can see the length is 6in. Because it is a rectangle, the opposite side is also 6in.
We can also see the width of the rectangle is 3in. Because it is a rectangle, the opposite side is also 3in.
Knowing this, we can substitute into the formula. We get
Example Question #581 : Plane Geometry
Use the following rectangle to solve the problem:
Find the perimeter.
To find the perimeter of a rectangle, we will use the following formula:
Where a, b, c, and d are the lengths of the sides of the rectangle.
Now, given the rectangle
we can see the length is 11in. Because it is a rectangle, the opposite side is also 11in.
The width is 5in. Because it is a rectangle, the opposite side is also 5in.
So, we can substitute.
Example Question #582 : Geometry
What is the width of the rectangle if the perimeter is 
The formula for perimeter of a rectangle is
To solve for the width we can plug our known values into the equation.
Subtract 
Divide 
Example Question #81 : Apply Area And Perimeter Formulas For Rectangles: Ccss.Math.Content.4.Md.A.3
What is the length of a room with a perimeter of 
We have the perimeter and the width, so we can plug those values into our equation and solve for our unknown.
Subtract 
Divide 
Example Question #5741 : Ssat Elementary Level Quantitative (Math)
Emily is digging a garden in her backyard that is 
The formula for perimeter of a rectangle is
To solve for the perimeter we can plug our known values into the equation.
Example Question #71 : Quadrilaterals
Angela has a garden that she wants to put a fence around. How much fencing will she need if her garden is 
The fence is going around the garden, so this is a perimeter problem.
Example Question #201 : Quadrilaterals
David wants to put a fence around a garden in his backyard. How much fencing will he need if his garden is 
The fence is going around the backyard, so this is a perimeter problem.
Example Question #581 : Plane Geometry
The altitude of a triangle is given as 
The area of a triangle is given by 
altitude
base 
Therefore:
Area
Certified Tutor
Certified Tutor
All SSAT Elementary Level Math Resources
