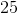All SSAT Elementary Level Math Resources
Example Questions
Example Question #231 : Data Analysis And Probability
Use the chart below to answer the question.

How many students have pets in Mr. Ray's class and Ms. Hen's class?
Each square represents students. Mr. Ray's bar has squares in it, which means he has students with pets (). Ms. Hen's bar has squares in it, which means she has students with pets ().
To find the total in both classes we add.
Example Question #232 : Data Analysis And Probability
Use the chart below to answer the question.

How many students have pets in Ms. Smith's class and Ms. Hen's class?
Each square represents students. Ms. Smith's bar has squares in it, which means she has students with pets (). Ms. Hen's bar has squares in it, which means she has students with pets ().
To find the total in both classes we add.
Example Question #11 : Answer Questions Using Information From A Bar Graph: Ccss.Math.Content.3.Md.B.3
Use the chart below to answer the question.

How many students in first grade have a sibling?
Each square represents students. The first grade bar has squares in it. That means we can take to find our total.
Example Question #234 : Data Analysis And Probability
Use the chart below to answer the question.

How many students in second grade have a sibling?
Each square represents students. The second grade bar has squares in it. That means we can take to find our total.
Example Question #235 : Data Analysis And Probability
Use the chart below to answer the question.

How many students in third grade have a sibling?
Each square represents students. The third grade bar has squares in it. That means we can take to find our total.
Example Question #236 : Data Analysis And Probability
Use the chart below to answer the question.

How many more students have a sibling in the first grade group than the third grade group?
Each square represents students. The first grade bar has squares in it, which means there are students who have a sibling ().The third grade bar has squares in it, which means there are students who have a sibling ().
To find the difference we subtract.
Example Question #237 : Data Analysis And Probability
Use the chart below to answer the question.

How many more students have a sibling in the first grade group than the fourth grade group?
Each square represents students. The first grade bar has squares in it, which means there are students who have a sibling ().The fourth grade bar has squares in it, which means there are students who have a sibling ().
To find the difference we subtract.
Example Question #238 : Data Analysis And Probability
Use the chart below to answer the question.

How many more students have a sibling in the fourth grade group than the third grade group?
Each square represents students. The fourth grade bar has squares in it, which means there are students who have a sibling ().The third grade bar has squares in it, which means there are students who have a sibling ().
To find the difference we subtract.
Example Question #239 : Data Analysis And Probability
Use the chart below to answer the question.

How many more students have a sibling in the second grade group than the third grade group?
Each square represents students. The second grade bar has squares in it, which means there are students who have a sibling ().The third grade bar has squares in it, which means there are students who have a sibling ().
To find the difference we subtract.
Example Question #240 : Data Analysis And Probability
Use the chart below to answer the question.

How many more students have a sibling in the second grade group than the first grade group?
Each square represents students. The second grade bar has squares in it, which means there are students who have a sibling ().The first grade bar has squares in it, which means there are students who have a sibling ().
To find the difference we subtract.
Certified Tutor
Certified Tutor
All SSAT Elementary Level Math Resources