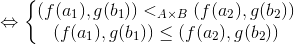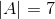Call Now to Set Up Tutoring:

(888) 888-0446

Set Theory : Set Theory

Study concepts, example questions & explanations for Set Theory

Create An Account

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Natural Numbers, Integers, And Real Numbers

What is the correct expression of the relationships between the sets comprised of natural numbers, real numbers, and integers?

Possible Answers:

$\mathbb{R}\subseteq\mathbb{Z}\subseteq \mathbb{N}$

$\mathbb{N}=\mathbb{Z}\subseteq \mathbb{R}$

$\mathbb{N}\subseteq\mathbb{Z}\subseteq \mathbb{R}$

$\mathbb{Z}\subseteq\mathbb{N}\subseteq \mathbb{R}$

$\mathbb{N}\subseteq\mathbb{Z}=\mathbb{R}$

Correct answer:

$\mathbb{N}\subseteq\mathbb{Z}\subseteq \mathbb{R}$

Explanation:

The natural numbers are defined as $\mathbb{N}=\left \{ 0,1,2,3,...\right \}$ , the integers are defined as $\mathbb{Z}=\left \{ ...-3,-2,-1,0,1,2,3,...\right \}$ , and the real numbers ( $\mathbb{R}$ ) are defined as the set of all non-complex numbers. As such, $\mathbb{N}$ is a subset of $\mathbb{Z}$ , and $\mathbb{Z}$ is a subset of $\mathbb{R}$ .

Report an Error

Example Question #21 : Set Theory

Determine if the following statement is true or false:

Let A_1 and A_2 be well ordered and order isomorphic sets. If B_1 and B_2 are also order isomorphic sets, then $A_1\times B_1$ and $A_2\times B_2$ are also order isomorphic.

Possible Answers:

False

True

Correct answer:

True

Explanation:

This is a theorem for well ordered sets and the proof is as follows.

First identify what is given in the statement.

1. The sets are onto order isomorphisms

$f:A_1\rightarrow A_2$ and $g:B_1\rightarrow B_2$

2. The goal is to make an onto order isomorphism. Let us call it .

$t:A_1\times B_1 \rightarrow A_2\times B_2$

Thus, can be defined as the function,

$\\t:A_1\times B_1\rightarrow A_2\times B_2 \\t(a,b)=(f(a),g(b))$

To show is a well defined, one-to-one, function on $A_1\times B_1$ since and are one-to-one, the following is performed.

$t(a,b)=t(u,v)\Rightarrow(f(a),g(b))=(f(u),g(v))$

$\\\Rightarrow f(a)=f(u), g(b)=g(v) \\\Rightarrow a=u, b=v \\\Rightarrow (a,b)=(u,v)$

Thus, is one-to-one.

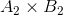
Now to prove in onto $A_2\times B_2$ if $(a,b)\ \epsilon\ A_2\times B_2$

a=f(u), b=g(v)

for some

$u\ \epsilon\ A_1, v\ \epsilon\ B_1$

thus

t(u,v)=(a,b)

proving is onto $A_2 \times B_2$ .

Lastly prove ordering.

$(a_1,b_1)\leq_{A\times B}(a_2,b_2)\Leftrightarrow \left\{\begin{matrix} a_1<_aa_2\\ a_1=a_2, b+1\leq_{r}b_2 \end{matrix}\right.$

$\Leftrightarrow\left\{\begin{matrix} f(a_1)<_{A}f(a_2)\\ f(a_1)=f(a_2), g(b_1\leq_{r}g(b_2)) \end{matrix}\right.$

$\Leftrightarrow\left\{\begin{matrix} (f(a_1),g(b_1))<_{A\times B}(f(a_2),g(b_2))\\ (f(a_1),g(b_1))\leq(f(a_2), g(b_2)) \end{matrix}\right.$

Thus proving is isomorphic. Therefore the statement is true.

Report an Error

Example Question #22 : Set Theory

Given the set , calculate the cardinality.

$A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$

Possible Answers:

|A|=7

|A|=9

|A|=21

|A|=8

|A|=11

Correct answer:

|A|=7

Explanation:

Given a set , the cardinality is the number of elements in . This is also written as |W| .

Looking at this particular problem,

$A=\begin{Bmatrix} 3,7,5,4,9,11,24 \end{Bmatrix}$

Therefore the number of elements in a is,

|A|=7

Report an Error

Example Question #2 : Cardinal Numbers

Given the set , calculate the cardinality.

$A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$

Possible Answers:

$|A|=\frac{a+e}{7}$

|A|=c

|A|=a

|A|=5

|A|=7

Correct answer:

|A|=5

Explanation:

Given a set , the cardinality is the number of elements in . This is also written as |W| .

Looking at this particular problem,

$A=\begin{Bmatrix} a,a,b,c,d,e,e \end{Bmatrix}$

First, rewrite the set to depict a more accurate description of the space.

$A=\begin{Bmatrix} a,b,c,d,e \end{Bmatrix}$

Therefore, counting up the number of elements, results in the following cardinality,

|A|=5

Report an Error

View Tutors

Beth
Certified Tutor

Sam Houston State University, Bachelor of Science, Education.

View Tutors

Anne
Certified Tutor

Vassar College, Bachelor in Arts, Drama and Dance Teacher Education. Emerson College, Master of Arts, Theater Management.

View Tutors

Stewart
Certified Tutor

University of North Texas, Bachelor of Science, Physical Education Teaching and Coaching. University of North Texas, Bachelor...

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Los Angeles, French Tutors in Denver, Chemistry Tutors in San Francisco-Bay Area, Calculus Tutors in San Diego, Statistics Tutors in Houston, Computer Science Tutors in Philadelphia, SAT Tutors in Los Angeles, Reading Tutors in Los Angeles, Calculus Tutors in Dallas Fort Worth, GRE Tutors in San Diego

Popular Courses & Classes

SSAT Courses & Classes in Denver, SAT Courses & Classes in Los Angeles, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in New York City, SAT Courses & Classes in Philadelphia, GRE Courses & Classes in Washington DC, Spanish Courses & Classes in Chicago, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles, ACT Test Prep in Boston, SSAT Test Prep in Boston, MCAT Test Prep in Atlanta, SAT Test Prep in Boston, GRE Test Prep in Chicago, GRE Test Prep in New York City, SAT Test Prep in New York City, GMAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Set Theory : Set Theory

Study concepts, example questions & explanations for Set Theory

All Set Theory Resources

Example Questions

Example Question #3 : Natural Numbers, Integers, And Real Numbers

Example Question #21 : Set Theory

Example Question #22 : Set Theory

Example Question #2 : Cardinal Numbers

All Set Theory Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: