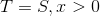Call Now to Set Up Tutoring:

(888) 888-0446

Set Theory : Set Theory

Study concepts, example questions & explanations for Set Theory

Create An Account

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Relations, Functions And Cartesian Product

Determine if the following statement is true or false:

If be the set defined as,

$A=\begin{Bmatrix} x,\begin{Bmatrix} x,y,z \end{Bmatrix}, \begin{Bmatrix} x,z \end{Bmatrix} \end{Bmatrix}$

then $x\subseteq A$ .

Possible Answers:

True

False

Correct answer:

True

Explanation:

Given is the set defined as,

$A=\begin{Bmatrix} x,\begin{Bmatrix} x,y,z \end{Bmatrix}, \begin{Bmatrix} x,z \end{Bmatrix} \end{Bmatrix}$

to state that $x\subseteq A$ , every element in must contain .

Looking at the elements in is is seen that all three elements in fact do contain therefore $x\subseteq A$ .

Thus, the answer is True.

Report an Error

Example Question #2 : Relations, Functions And Cartesian Product

For a bijective function from set to set defined by $f:A \rightarrow B$ , which of the following does NOT need to be true?

Possible Answers:

Every element of must map to one or more elements of .

No element of may map to multiple elements of .

All of the conditions here must be true.

No element of may map to multiple elements of .

Correct answer:

All of the conditions here must be true.

Explanation:

For a bijective function, every element in set must map to exactly one element of set , so that every element in set has exactly one corresponding element in set . All of the conditions presented must be true in order to satisfy this definition.

Report an Error

Example Question #1 : Relations, Functions And Cartesian Product

For an injective function from set to set defined by $f:A \rightarrow B$ , which of the following does NOT need to be true?

Possible Answers:

Every element of must map to one or more elements of .

No element of may map to multiple elements of .

All of the conditions here must be true.

No element of may map to multiple elements of .

Every element of must map to one or more elements of .

Correct answer:

Every element of must map to one or more elements of .

Explanation:

For an injective function, every element of must map to exactly one element of . Additionally, every element in must map to a different element in so that no element in has multiple pairings to elements in . It is not necessary for all elements of to be connected to an element in .

Report an Error

Example Question #5 : Relations, Functions And Cartesian Product

For a surjective function from set to set defined by $f:A \rightarrow B$ , which of the following does NOT need to be true?

Possible Answers:

All of the conditions here must be true.

Every element of must map to one or more elements of .

No element of may map to multiple elements of .

Every element of must map to one or more elements of .

Correct answer:

No element of may map to multiple elements of .

Explanation:

For a surjective function, every element of must map to exactly one element of . Additionally, all elements of to be paired with an element in , even if one or more elements of is connected to multiple elements in .

Report an Error

Example Question #4 : Relations, Functions And Cartesian Product

For which of the following pairs is the cardinality of the two sets equal?

Possible Answers:

$\left \{ 0\right \},\varnothing$

and , where there exists an injective, non-surjective function $f:A\rightarrow B$ .

$\mathbb{R},\mathbb{N}$

$\left \{ 1,2,3\right \},\left \{ 0,1,2,3\right \}$

$\left \{ x|x\in \mathbb{N}\right \},\left \{ 2y|y\in \mathbb{N}\right \}$

Correct answer:

$\left \{ x|x\in \mathbb{N}\right \},\left \{ 2y|y\in \mathbb{N}\right \}$

Explanation:

The cardinality of $\mathbb{R}$ ( $\mathfrak{c}$ ) is greater than that of $\mathbb{N}$ ( $\aleph_{0}$ ,) as established by Cantor's first uncountability proof, which demonstrates that $\mathfrak{c}=2^{\aleph_{0}}>\aleph_{0}$ . The cardinality of the empty set is 0, while the cardinality of $\left \{ 0\right \}$ is 1. $\left | \left \{ 1,2,3\right \} \right |=3$ , while $\left | \left \{ 1,2,3,4\right \} \right |=4$ . For sets and , where there exists an injective, non-surjective function $f:A\rightarrow B$ , must have more elements than , otherwise the function would be bijective (also called injective-surjective). Finally, for $\left \{ x|x\in \mathbb{N}\right \},\left \{ 2y|y\in \mathbb{N}\right \}$ , the cardinality of both sets is equal to the cardinality of $\mathbb{N}$ .

Report an Error

Example Question #3 : Relations, Functions And Cartesian Product

What type of function is $f:\mathbb{Z}\rightarrow \mathbb{N}$ where $x \mapsto \left |x \right |$ ?

Possible Answers:

Surjective

Bijective

Injective

None of these answers is correct.

Correct answer:

Surjective

Explanation:

Because multiple elements of $\mathbb{Z}$ can map to a single element of $\mathbb{N}$ (e.g. -2 and 2 map to 2), this function is surjective.

Report an Error

Example Question #4 : Relations, Functions And Cartesian Product

What type of function is $f:\mathbb{N}\rightarrow \mathbb{Z}$ where $x \mapsto x^2$ ?

Possible Answers:

Surjective

Bijective

None of these answers is correct.

Injective

Correct answer:

Injective

Explanation:

Because every element of $\mathbb{N}$ maps to a single element of $\mathbb{Z}$ , but there are many elements of $\mathbb{Z}$ that do not pair with any element of $\mathbb{N}$ , this function is injective.

Report an Error

Example Question #5 : Relations, Functions And Cartesian Product

What type of function is $f:\mathbb{Z}\rightarrow \mathbb{R}$ where $x \mapsto \sqrt{x}$ ?

Possible Answers:

None of these answers is correct.

Surjective

Injective

Bijective

Correct answer:

None of these answers is correct.

Explanation:

Because this operation is not defined for the negative elements of $\mathbb{Z}$ , it is either considered to be a partial function or not a function at all! Each element in the sub-domain of $\mathbb{Z}$ for which the operation is defined maps to exactly 1 element in $\mathbb{R}$ ; however, many elements of $\mathbb{R}$ are not paired to any element in this sub-domain of $\mathbb{Z}$ , thus the function could be considered a partial injective function.

Report an Error

Example Question #11 : Set Theory

Are the sets and equal?

$\\T=\begin{Bmatrix} x|x\ \epsilon\ \mathbb{Z} \end{Bmatrix} \\S=\begin{Bmatrix} 2n|n\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

Possible Answers:

T= S, x>0

$T\neq S$

T= S

$T= S, x\geq0$

T= S, x<0

Correct answer:

$T\neq S$

Explanation:

To determine if two sets are equal to each other it must be proven that each set contains the same elements.

Recall the following terminology,

$\\\mathbb{Z}=\text{Integers}{\begin{Bmatrix} ...,-2,-1,0,1,2,... \end{Bmatrix}} \\\mathbb{R}=\text{Reals} \\\mathbb{N}=\text{Naturals} {\begin{Bmatrix} 0,1,2,... \end{Bmatrix}}$

Now, identify the elements in each set.

$\\T=\begin{Bmatrix} x|x\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

This means all integers are elements of .

Let x=3 ,

$\\S=\begin{Bmatrix} 2n|n\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

is the value for all integers.

Therefore if n=3 the element in is,

2(n)=2(3)=6

This means that all elements in will be divisible by two and thus be an even number therefore, 3 will never be an element in .

Thus, it is concluded that

$T\neq S$

Report an Error

Example Question #2 : Natural Numbers, Integers, And Real Numbers

Are the sets and equal?

$\\T=\begin{Bmatrix} x|x\ \epsilon\ \mathbb{Z} \end{Bmatrix} \\S=\begin{Bmatrix} 1+n|n\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

Possible Answers:

$T\neq S, x\geq0$

T= S, x>0

T= S, x<0

T=S

$T\neq S$

Correct answer:

T=S

Explanation:

To determine if two sets are equal to each other it must be proven that each set contains the same elements.

Recall the following terminology,

$\\\mathbb{Z}=\text{Integers}{\begin{Bmatrix} ...,-2,-1,0,1,2,... \end{Bmatrix}} \\\mathbb{R}=\text{Reals} \\\mathbb{N}=\text{Naturals} {\begin{Bmatrix} 0,1,2,... \end{Bmatrix}}$

Now, identify the elements in each set.

$\\T=\begin{Bmatrix} x|x\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

This means all integers are elements of .

Let x=3 ,

$\\S=\begin{Bmatrix} 1+n|n\ \epsilon\ \mathbb{Z} \end{Bmatrix}$

is the value 1+n for all integers.

Therefore if n=3 the element in is,

1+n=1+3=4

Since four also belongs to $\mathbb{Z}$ this means that all elements in will be the same as those in .

Thus, it is concluded that

T=S

Report an Error

View Tutors

Renetta
Certified Tutor

Langston University, Bachelor of Science, Education of Individuals in Elementary Special Education Programs.

View Tutors

Deborah
Certified Tutor

Saint Mary's College, Bachelor of Science, Organizational Leadership. Solano Community College, Associate in Science, Busines...

View Tutors

Sienna
Certified Tutor

Russell sage college, Master of Science, Forensic Psychology.

All Set Theory Resources

7 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Phoenix, Algebra Tutors in San Diego, ISEE Tutors in Phoenix, Statistics Tutors in San Francisco-Bay Area, ACT Tutors in New York City, Reading Tutors in Dallas Fort Worth, Computer Science Tutors in Los Angeles, Biology Tutors in Washington DC, LSAT Tutors in Philadelphia, French Tutors in Seattle

Popular Courses & Classes

GRE Courses & Classes in Boston, LSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Atlanta, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Houston, ISEE Courses & Classes in Atlanta, SAT Courses & Classes in Denver, ISEE Courses & Classes in Chicago, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in Miami, MCAT Test Prep in Denver, LSAT Test Prep in Atlanta, ISEE Test Prep in Houston, SAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Boston, ISEE Test Prep in Dallas Fort Worth, GMAT Test Prep in Houston, SAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Set Theory : Set Theory

Study concepts, example questions & explanations for Set Theory

All Set Theory Resources

Example Questions

Example Question #1 : Relations, Functions And Cartesian Product

Example Question #2 : Relations, Functions And Cartesian Product

Example Question #1 : Relations, Functions And Cartesian Product

Example Question #5 : Relations, Functions And Cartesian Product

Example Question #4 : Relations, Functions And Cartesian Product

Example Question #3 : Relations, Functions And Cartesian Product

Example Question #4 : Relations, Functions And Cartesian Product

Example Question #5 : Relations, Functions And Cartesian Product

Example Question #11 : Set Theory

Example Question #2 : Natural Numbers, Integers, And Real Numbers

All Set Theory Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: