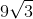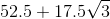We can model the side lengths of the triangle as 3x, 4x, and 5x. We know that perimeter is 3x+4x+5x=48, which implies that x=4. This tells us that the legs of the right triangle are 3x=12 and 4x=16, therefore the area is A=1/2 bh=(1/2)(12)(16)=96.

The base is equal to 6.

The height of an quilateral triangle is equal to , where is the length of the base.

The altitude of a right triangle from the vertex of its right angle - which, here, is  - divides the triangle into two triangles similar to each other and to the large triangle. From the Pythagorean Theorem, the hypotenuse of  has length

.

The similarity ratio of  to  is the ratio of the lengths of the hypotenuses:

The ratio of the areas of two similar triangles is the square of their similarity ratio, which here is 

Therefore, the area of  is

the overall area of . This makes  the closest response.

Because the perimeter is equal to the sum of the lengths of the three sides of a triangle, we can add the three expressions for the lengths and set them equal to 40.

Perimeter:

Simplify the x terms.

Simplify the constants.

Subtract 8 from both sides.

Divide by 4

One side is 8.

The second side is

.

The third side is

.

Thus, the sides of the triangle are 8, 15, and 17.

The question asks us for the area of the triangle, which is given by the formula (1/2)bh. We are told it is a right triangle, so we can use one of the legs as the base, and the other leg as the height, since the legs will intersect at right angles. The legs of the right triangle must be the smallest sides (the longest must be the hypotenuse), which in this case are 8 and 15. So, let's assume that 8 is the base and 15 is the height. 

The area of a triangle is (1/2)bh. We can substitute 8 and 15 for b and h.

.

The answer is 60 units squared.

The triangle in question can be drawn as the following:

The lengths of the legs of the triangle are 12, the distance from the origin to , and 8, the distance from the origin to . The area of a right triangle is equal to half the product of the lengths of the legs, so set  in the formula:

Drawing points gives sides of a right triangle of 4, 5, and an unknown hypotenuse.

Using the pythagorean theorem we find that the hypotenuse is .

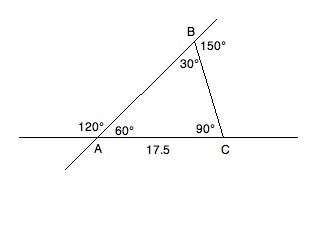
Consult the diagram above while reading the solution. Because of what we know about supplementary angles, we can fill in the inner values of the triangle. Angles A and B can be found by the following reductions:

A + 120 = 180; A = 60

B + 150 = 180; B = 30

Since we know A + B + C = 180 and have the values of A and B, we know:

60 + 30 + C = 180; C = 90

This gives us a 30:60:90 triangle. Now, since 17.5 is across from the 30° angle, we know that the other two sides will have to be √3 and 2 times 17.5; therefore, our perimeter will be as follows:

The figure shows a right triangle. The acute angles of a right triangle have measures whose sum is , so

Substituting  for :

This makes  a 45-45-90 triangle.

By the 45-45-90 Triangle Theorem, legs  and  are of the same length, so

.

Also by the 45-45-90 Triangle Theorem, the length of hypotenuse is equal to that of leg  multiplied by . Therefore, 

.

The perimeter of the triangle is 

The figure shows a right triangle. The acute angles of a right triangle have measures whose sum is , so

Substituting  for :

This makes  a 45-45-90 triangle. By the 45-45-90 Triangle Theorem, the length of leg  is equal to that of hypotenuse , the length of which is 12, divided by . Therefore,

Rationalize the denominator by multiplying both halves of the fraction by :

By the same reasoning, .

The perimeter of the triangle is 

This problem is solved using the Pythagorean theorem  .  In this formula  and  are the legs of the right triangle while  is the hypotenuse.

Using the labels of our triangle we have: