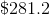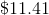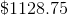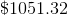To expand our number, we should look at the exponent provided. We see that our exponent raises  to the power of positive . Since the exponent is positive, we know that we need to move our decimal to the right five places. Doing that yields our answer, . 

To put a number in scientific notation, we want to have a number with one digit in the units place followed by a decimal point and any subsequent digits. That number is then multiplied by ten raised to a power that matches how many places we moved the decimal point in the original number. 

To write this number in scientific notation, we want our expression to be . When we move the decimal place to the left in  to create , we move it six places to the left. 

Therefore, this number in scientific notation is .

Which of the following is equivalent to ?

To solve this problem, all we need to do is move the decimal point.

Because we have a negative exponent (-3), we have to move our decimal point to the left.

Because our exponent is 3, we will move the decimal point 3 to the left:

Making our answer:

Each year, you can calculate your interest by multiplying the principle () by . For one year, this would be:

For two years, it would be:

, which is the same as 

Therefore, you can solve for a five year period by doing:

Using your calculator, you can expand the  into a series of multiplications. This gives you , which is closest to . 

It is easiest to break this down into steps. For each year, you will multiply by  to calculate the new value. Therefore, let's make a chart:

After year 1: ; Total interest: 

After year 2: ; Let us round this to ; Total interest: 

After year 3: ; Let us round this to ; Total interest: 

Thus, the positive difference of the interest from the last period and the interest from the first period is: 

First, break the problem into two segments: the amount Jack invests in the high-yield savings, and the amount Jack invests in the simple interest account (10,000 and 5,000 respectively).

Now let's work with the high-yield savings account. $10,000 is invested at an annual rate of 8%, compounded quarterly. We can use the compound interest formula to solve:

Plug in the values given:

Therefore, Jack makes $824.32 off his high-yield savings account. Now let's calculate the other interest:

Add the two together, and we see that Jack makes a total of,  off of his investments.

The first step is to convert the depreciation rate into a decimal. . Now lets recall the exponential decay model. , where  is the starting amount of money,  is the annual rate of decay, and  is time (in years). After substituting, we get

Multiplying like bases means add the exponents, so x+4 = 12, or x = 8.

Raising a power to a power means multiply the exponents, so 3y = 15, or y = 5.

x - y = 8 - 5 = 3.

The first step is to express both sides of the equation with equal bases, in this case 3. The equation becomes 3^3p = 3^2q. So then 3p = 2q, and q = (3/2)p is our answer. 

27^2/3 is 27 squared and cube-rooted. We want to pick the easier operation first. Here that is the cube root. To see that, try both operations. 

27^2/3 = (27²)^1/3 = 729^1/3 OR

27^2/3 = (27^1/3)² = 3²

Obviously 3² is much easier. Either 3² or 729^1/3 will give us the correct answer of 9, but with 3² it is readily apparent.