All SAT Math Resources
Example Questions
Example Question #3 : Variables
Find the product:
Find the product:
Step 1: Multiply the numerators and denominators using the properties of exponents. (When multiplying exponents, add them.)
Step 2: Simplify the expression.
Example Question #2131 : Sat Mathematics
Phillip can paint 
Every minute Phillip completes another 
There are 60 minutes in an hour, and he paints for 2.5 hours. Multiply to find the total number of minutes.
If he completes 

Example Question #2132 : Sat Mathematics
The value of 








Let's consider the general case when y varies directly with x. If y varies directly with x, then we can express their relationship to one another using the following formula:
y = kx, where k is a constant.
Therefore, if y varies directly as the square of x and the cube of z, we can write the following analagous equation:
y = kx2z3, where k is a constant.
The problem states that y = 24 when x = 1 and z = 2. We can use this information to solve for k by substituting the known values for y, x, and z.
24 = k(1)2(2)3 = k(1)(8) = 8k
24 = 8k
Divide both sides by 8.
3 = k
k = 3
Now that we have k, we can find y if we know x and z. The problem asks us to find y when x = 3 and z = 1. We will use our formula for direct variation again, this time substitute values for k, x, and z.
y = kx2z3
y = 3(3)2(1)3 = 3(9)(1) = 27
y = 27
The answer is 27.
Example Question #2133 : Sat Mathematics
In a growth period, a population of flies triples every week. If the original population had 3 flies, how big is the population after 4 weeks?
We know that the initial population is 3, and that every week the population will triple.
The equation to model this growth will be 



In this case, the equation will be 
Alternatively, you can evaluate for each consecutive week.
Week 1:
Week 2:
Week 3:
Week 4:
Example Question #4 : Direct And Inverse Variation


Which of the following is a true statement? (Assume all quantities are positive)












If 


By substitution,
Taking the square root of both sides:
Taking 

meaning that 

Example Question #5 : Direct And Inverse Variation





Which of the following is a true statement?












The volume of a cone can be calculated from the radius of its base 






Square both sides:
If we take 

and 

Example Question #1 : Direct And Inverse Variation


![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500721/gif.latex)
Which of the following is a true statement?












The volume of a sphere can be calculated from its radius as follows:
Therefore, squaring both sides, we get
Substituting:
If we let the constant of variation be 

and 


Example Question #2134 : Sat Mathematics
The temperature at the surface of the ocean is 



This may seem confusing, but is pretty straightforward.
Thus, for every 125 meters below the surface, the temperature decreases by one degree.
To find how much it decreases with every 100 meters, we need to do the following:
Thus, the temperature decreases by 
Example Question #1 : How To Use The Inverse Variation Formula
The square of 





When two quantities vary inversely, their products are always equal to a constant, which we can call k. If the square of x and the cube of y vary inversely, this means that the product of the square of x and the cube of y will equal k. We can represent the square of x as x2 and the cube of y as y3. Now, we can write the equation for inverse variation.
x2y3 = k
We are told that when x = 8, y = 8. We can substitute these values into our equation for inverse variation and then solve for k.
82(83) = k
k = 82(83)
Because this will probably be a large number, it might help just to keep it in exponent form. Let's apply the property of exponents which says that abac = ab+c.
k = 82(83) = 82+3 = 85.
Next, we must find the value of y when x = 1. Let's use our equation for inverse variation equation, substituting 85 in for k.
x2y3 = 85
(1)2y3 = 85
y3 = 85
In order to solve this, we will have to take a cube root. Thus, it will help to rewrite 8 as the cube of 2, or 23.
y3 = (23)5
We can now apply the property of exponents that states that (ab)c = abc.
y3 = 23•5 = 215
In order to get y by itself, we will have the raise each side of the equation to the 1/3 power.
(y3)(1/3) = (215)(1/3)
Once again, let's apply the property (ab)c = abc.
y(3 • 1/3) = 2(15 • 1/3)
y = 25 = 32
The answer is 32.
Example Question #9 : Direct And Inverse Variation





Which of the following is true about 























We can square both sides to obtain:



By substitution,

Using 



Certified Tutor
All SAT Math Resources




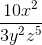




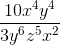












































![W = \sqrt[3]{V}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500726/gif.latex)
![W ^{6 }= \left (\sqrt[3]{V} \right ) ^{6}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/500727/gif.latex)



























