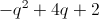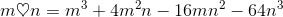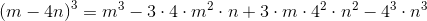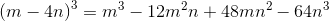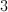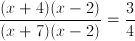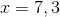All SAT Math Resources
Example Questions
Example Question #11 : Polynomials


Evaluate 

Additionally,


Using the product of radicals property, we see that
and



and
Substituting for 


Example Question #2161 : Sat Mathematics
Simplify the following expression:
This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.
Add like terms together:

Combine these terms into one expression to find the answer:
Example Question #12 : Polynomials
Define an operation 
For all real 
How else could this operation be defined?

Applying the rules of exponents to simplify this:
Therefore, the correct choice is that, alternatively stated,

Example Question #2162 : Sat Mathematics
Solve for 
Factor the expression
numerator: find two numbers that add to 2 and multiply to -8 [use 4,-2]
denominator: find two numbers that add to 5 and multiply to -14 [use 7,-2]
new expression:
Cancel the 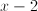
Example Question #2161 : Sat Mathematics
If 〖(x+y)〗2 = 144 and 〖(x-y)〗2 = 64, what is the value of xy?
18
22
16
20
20
We first expand each binomial to get x2 + 2xy + y2 = 144 and x2 - 2xy + y2 = 64. We then subtract the second equation from the first to find 4xy = 80. Finally, we divide each side by 4 to find xy = 20.
Example Question #21 : Polynomials
Solve each problem and decide which is the best of the choices given.
What are the zeros of the following trinomial?
First factor out a 


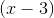
Set everything equal to zero and you get 



Example Question #2163 : Sat Mathematics
Subtract 

Step 1: We need to read the question carefully. It says subtract from. When you see the word "from", you read the question right to left.
I am subtracting the left equation from the right equation.
Step 2: We need to write the equation on the right minus the equation of the left.
Step 3: Distribute the minus sign in front of the parentheses:
Step 4: Combine like terms:
Step 5: Put all the terms together, starting with highest degree. The degree of the terms is the exponent. Here, the highest degree is 2 and lowest is zero.
The final equation is 
Example Question #6 : Factoring Polynomials
What is a possible value for x in x2 – 12x + 36 = 0 ?
There is not enough information
6
–6
2
6
You need to factor to find the possible values for x. You need to fill in the blanks with two numbers with a sum of -12 and a product of 36. In both sets of parenthesis, you know you will be subtracting since a negative times a negative is a positive and a negative plus a negative is a negative
(x –__)(x –__).
You should realize that 6 fits into both blanks.
You must now set each set of parenthesis equal to 0.
x – 6 = 0; x – 6 = 0
Solve both equations: x = 6
Example Question #2162 : Sat Mathematics
If r and t are constants and x2 +rx +6=(x+2)(x+t), what is the value of r?
5
6
7
It cannot be determined from the given information.
5
We first expand the right hand side as x2+2x+tx+2t and factor out the x terms to get x2+(2+t)x+2t. Next we set this equal to the original left hand side to get x2+rx +6=x2+(2+t)x+2t, and then we subtract x2 from each side to get rx +6=(2+t)x+2t. Since the coefficients of the x terms on each side must be equal, and the constant terms on each side must be equal, we find that r=2+t and 6=2t, so t is equal to 3 and r is equal to 5.
Example Question #2164 : Sat Mathematics
Solve for 
First, add 4 to both sides:
Divide both sides by 2:
All SAT Math Resources