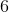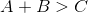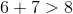An altitude drawn in an equilateral triangle will form two 30-60-90 triangles. The height of equilateral triangle is the length of the longer leg of the 30-60-90 triangle. The length of the equilateral triangle's side is the length of the hypotenuse of the 30-60-90.

The ratio of the length of the hypotenuse to the length of the longer leg of a 30-60-90 triangle is  

The length of the longer leg of the 30-60-90 triangle in this problem is

Using this ratio, we find that the length of this triangle's hypotenuse is 4. Thus the perimeter of the equilateral triangle will be 4 multiplied by 3, which is 12.

The area of a triangle is (1/2)*base*height. We know that the area = 15 cm, and the base is 5 cm, so:

15 = 1/2 * 5 * height

3 = 1/2 * height

6 = height

The sum of the lengths of the shortest sides of a triangle cannot be less than the third side.

3 + 5 = 8 < 9, so 3 can't be a value of x.

Because the triangle is an equilateral triangle, you know that all sides have the same length, so all sides have the length of 4. Draw the triangle and label all sides as 4. Next, draw a point in the middle of one of the sides, and label each side as 2. Draw a line segment from the midpoint that you just created to the opposite angle of the triangle. That line segment is the height of the triangle. You can solve for it by using the Pythagorean theorem.

The Pythagorean theorem states that

In our scenario a = 2, c = 4, and you are solving for b. After plugging the numbers into the formula you get

and then 

and then 

and then 

Therefore, the height of the triangle is  

If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.

The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.

We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√3.

In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s²/4.

An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side.  So A_triangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm².

Recall that an equilateral triangle also obeys the rules of isosceles triangles.   That means that our triangle can be represented as having a height that bisects both the opposite side and the angle from which the height is "dropped."  For our triangle, this can be represented as:

Now, although we do not yet know the height, we do know from our 30-60-90 regular triangle that the side opposite the 60° angle is √3 times the length of the side across from the 30° angle. Therefore, we know that the height is 3√3.

Now, the area of a triangle is (1/2)bh. If the height is 3√3 and the base is 6, then the area is (1/2) * 6 * 3√3 = 3 * 3√3 = 9√(3).

Perimeter of hexagon =  = perimeter of triangle

 = side of the triangle

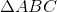
The sum of the lengths of any two sides of a triangle must be greater than the length of third side.

Therefore, because 

and

, the correct answer must be .