SAT Math : SAT Mathematics
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?
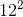
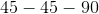
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A right triangle has one side equal to 5 and its hypotenuse equal to 14. Its third side is equal to:
12
9
13.07
171
14.87
13.07
The Pythagorean Theorem gives us a2 + b2 = c2 for a right triangle, where c is the hypotenuse and a and b are the smaller sides. Here a is equal to 5 and c is equal to 14, so b2 = 142 – 52 = 171. Therefore b is equal to the square root of 171 or approximately 13.07.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
Which of the following could NOT be the lengths of the sides of a right triangle?
8, 15, 17
14, 48, 50
12, 16, 20
5, 12, 13
5, 7, 10
5, 7, 10
We use the Pythagorean Theorem and we calculate that 25 + 49 is not equal to 100.
All of the other answer choices observe the theorem a2 + b2 = c2
Example Question #454 : Geometry
Which set of sides could make a right triangle?
4, 6, 9
9, 12, 15
10, 12, 16
6, 7, 8
9, 12, 15
By virtue of the Pythagorean Theorem, in a right triangle the sum of the squares of the smaller two sides equals the square of the largest side. Only 9, 12, and 15 fit this rule.
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A right triangle with a base of 12 and hypotenuse of 15 is shown below. Find x.
5.5
5
4
3.5
4.5
4
Using the Pythagorean Theorem, the height of the right triangle is found to be = √(〖15〗2 –〖12〗2) = 9, so x=9 – 5=4
Example Question #456 : Geometry
A right triangle has sides of 36 and 39(hypotenuse). Find the length of the third side
33
15
42
12 √6
33√2
15
use the pythagorean theorem:
a2 + b2 = c2 ; a and b are sides, c is the hypotenuse
a2 + 1296 = 1521
a2 = 225
a = 15
Example Question #81 : Triangles
Bob the Helicopter is at 30,000 ft. above sea level, and as viewed on a map his airport is 40,000 ft. away. If Bob travels in a straight line to his airport at 250 feet per second, how many minutes will it take him to arrive?
3 minutes and 20 seconds
1 hour and 45 minutes
3 minutes and 50 seconds
4 hours and 0 minutes
2 hours and 30 minutes
3 minutes and 20 seconds
Draw a right triangle with a height of 30,000 ft. and a base of 40,000 ft. The hypotenuse, or distance travelled, is then 50,000ft using the Pythagorean Theorem. Then dividing distance by speed will give us time, which is 200 seconds, or 3 minutes and 20 seconds.
Example Question #81 : Right Triangles
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
11
10
14
12
13
12
We can use the Pythagorean Theorem to solve for x.
92 + x2 = 152
81 + x2 = 225
x2 = 144
x = 12
Example Question #82 : Triangles
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Example Question #83 : Triangles
Solve for x.
6
12
2
7
6
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
Certified Tutor
All SAT Math Resources
