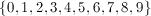We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Integers

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : How To Find The Next Term In An Arithmetic Sequence

An arithmetic sequence begins as follows:

$\sqrt{5} , \sqrt{10},...$

Give the next term of the sequence in simplest radical form.

Possible Answers:

$3 \sqrt{5}$

$2 \sqrt{5}$

$\sqrt{15}$

None of the other choices gives the correct response.

$2 \sqrt{10}$

Correct answer:

None of the other choices gives the correct response.

Explanation:

Since no perfect square integer greater than 1 divides evenly into 5 or 10, both of the first two terms of the sequence are in simplest form.

The common difference of an arithmetic sequence can be found by subtracting the first term from the second:

$d = a_{2} - a_{1}$

Setting $a_{1}= \sqrt{5}, a_{2}= \sqrt{10}$ :

$d = \sqrt{10} - \sqrt{5}$

Add this to the second term to obtain the desired third term:

$a_{3} = a_{2} +d =\sqrt{10} + ( \sqrt{10} - \sqrt{5}) = \sqrt{10} + \sqrt{10} - \sqrt{5} = 2\sqrt{10}- \sqrt{5}$

This is not among the given choices.

Report an Error

Example Question #4 : How To Find The Next Term In An Arithmetic Sequence

An arithmetic sequence begins as follows:

$\frac{1}{5} , \frac{1}{3} , ...$

Give the sixth term of the sequence in decimal form.

Possible Answers:

$0.\overline{8}$

$0.9\overline{3}$

$0.8\overline{6}$

0.8

0.875

Correct answer:

$0.8\overline{6}$

Explanation:

The common difference of an arithmetic sequence can be found by subtracting the first term from the second:

$d = a_{2} - a_{1}$

Setting $a_{1}= \frac{1}{5}, a_{2}= \frac{1}{3}$ :

$d = \frac{1}{3} - \frac{1}{5} = \frac{5}{15} - \frac{3}{15} = \frac{2}{15}$

The th term $a_{n}$ of an arithmetic sequence can be derived using the formula

$a_{n} = a_{1} + (n-1)d$

Setting $n = 6 , a_{1} = \frac{1}{5}= \frac{3}{15}, d = \frac{2}{15}$ :

$a_{n} = \frac{3}{15} + (6-1) \cdot \frac{2}{15}$

$= \frac{3}{15} +5 \cdot \frac{2}{15}$

$= \frac{3}{15} + \frac{10}{15}$

$= \frac{13}{15}$

The decimal equivalent of this can be found by dividing 13 by 15 as follows:

Division

The correct choice is $0.8\overline{6}$ .

Report an Error

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

An arithmetic sequence begins as follows:

4, 5 i ,...

Give the sixth term of the sequence.

Possible Answers:

-16+25i

-20 + 30 i

20+25 i

-20 + 25i

25+30i

Correct answer:

-16+25i

Explanation:

The common difference of an arithmetic sequence can be found by subtracting the first term from the second:

$d = a_{2} - a_{1}$

Setting $a_{1}= 4, a_{2}= 5i$ :

d = 5i - 4 = -4+5i

The th term $a_{n}$ of an arithmetic sequence can be derived using the formula

$a_{n} = a_{1} + (n-1)d$

Setting $a_{1}= 4, n = 6, d= -4+5i$

$a_{6} =4 + (6-1) ( -4+5i)$

=4 +5( -4+5i)

=4 +( -20+25i)

=(4 -20)+25i

=-16+25i

Report an Error

Example Question #811 : Arithmetic

Complete the sequence:

1, 8, 27, x, 125

Possible Answers:

150

335

400

125

Correct answer:

Explanation:

The pattern of this sequence is n^3 where represents the place of each number in the order of the sequence.

Here are our givens:

n^3

1^3 = 1 , our first term.

2^3 = 8 , our second term.

3^3 = 27 , our third term.

This means that our fourth term will be:

4^3 = 64 .

Report an Error

Example Question #1 : How To Find The Missing Number In A Set

Which number completes the following series: 1, 2, 4, 8, 16, 32, 64, _?

Possible Answers:

Not enough information

128

Correct answer:

128

Explanation:

All of the numbers in this series are 2^n-1. The number that we are looking for is the eighth number. So 2^8–1 = 2⁷ = 128.

Report an Error

Example Question #2 : How To Find The Missing Number In A Set

Alhough Danielle’s favorite flowers are tulips, she wants at least one each of three different kinds of flowers in her bouquet. Roses are twice as expensive as lilies and lilies are 25% of the price of tulips. If a rose costs $20 and Danielle only has $130, how many tulips can she buy?

Possible Answers:

Correct answer:

Explanation:

She can only buy 2 tulips at $80, because if she bought 3 she wouldn’t have enough to afford the other 2 kinds of flowers. She has to spend at least 30 dollars (20 + 10) on 1 rose and 1 lily.

Report an Error

Example Question #1 : How To Find The Missing Number In A Set

Which of the following is not a rational number?

Possible Answers:

1.75

√2

0.111...

.001

Correct answer:

√2

Explanation:

A rational number is a number that can be written in the form of a/b, where a and b are integers, aka a real number that can be written as a simple fraction or ratio. 4 of the 5 answer choices can be written as fractions and are thus rational.

5 = 5/1, 1.75 = 7/4, .001 = 1/1000, 0.111... = 1/9

√2 cannot be written as a fraction because it is irrational. The two most famous irrational numbers are √2 and pi.

Report an Error

Example Question #2 : Sets

Which set represents all the single-digits integers (0-9) that are either prime, a perfect square, or found in the number 68?

Possible Answers:

$\dpi{100} \small \left \{0,2,3,5,6,7,8 \right \}$

$\dpi{100} \small \left \{1,3,4,5,7,9 \right \}$

$\dpi{100} \small \left \{ 0,1,2,3,4,5,6,7,8,9 \right \}$

$\dpi{100} \small \left \{1,2,3,4,5,6,7,8,9 \right \}$

$\dpi{100} \small \left \{2,3,4,5,6,7,8,9 \right \}$

Correct answer:

$\dpi{100} \small \left \{ 0,1,2,3,4,5,6,7,8,9 \right \}$

Explanation:

The prime digits are 2, 3, 5, and 7.

The perfect square digits are 0, 1, 4, and 9.

The only digits not represent in these two groups are 6 and 8, which are, coincidentally, found in the number 68.

Report an Error

Example Question #1 : How To Find The Missing Number In A Set

If four different integers are selected, one from each of the following sets, what is the greater sum that these four integers could have?

W = {4, 6, 9, 10}

X = {4, 5, 8, 10}

Y = {3, 6, 7, 11}

Z = {5, 8, 10, 11}

Possible Answers:

Correct answer:

Explanation:

By observing each of these sets, we can easily determine the largest number in each; however, the problem is asking for us to find the greatest possible sum if we select four different integers, one from each set. The largest number is 11. We will either select this number from set Y or set Z.

We will select set

Y for the 11

because the next larger number in set

Z is 10, which is greater than the next largest number is set Y, 7.

We can use set Z for 10.

Because the 10 has already been selected, choosing the integer from W and X should be easy because 9 is the next largest integer from set W

and

8 is the next largest integer from set X.

11 + 10 + 9 + 8 = 38

Report an Error

Example Question #1 : Sets

A team has a win-loss ratio of $4:1$ . If the team wins six games in a row, the win-loss ratio will now be $6:1$ . How many losses did the team have initially?

Possible Answers:

$2$

$3$

$4$

$1$

$5$

Correct answer:

$3$

Explanation:

If a team's ratio of wins to losses increases from $4:1$ to $6:1$ by winning six games, they must have 12 wins initially and 3 losses.

Report an Error

View SAT Mathematics Tutors

Alexandra
Certified Tutor

Georgia State University, Bachelor of Fine Arts, Studio Art (Photography).

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in New York City, SAT Courses & Classes in Denver, ISEE Courses & Classes in Miami, SAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in Los Angeles, ACT Courses & Classes in New York City, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SAT Test Prep in Dallas Fort Worth, SAT Test Prep in Seattle, GRE Test Prep in San Francisco-Bay Area, ACT Test Prep in Washington DC, GMAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Los Angeles, GRE Test Prep in Atlanta, ACT Test Prep in Chicago, ACT Test Prep in Los Angeles, SSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Integers

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #5 : How To Find The Next Term In An Arithmetic Sequence

Example Question #4 : How To Find The Next Term In An Arithmetic Sequence

Example Question #1 : How To Find The Next Term In An Arithmetic Sequence

Example Question #811 : Arithmetic

Example Question #1 : How To Find The Missing Number In A Set

Example Question #2 : How To Find The Missing Number In A Set

Example Question #1 : How To Find The Missing Number In A Set

Example Question #2 : Sets

Example Question #1 : How To Find The Missing Number In A Set

Example Question #1 : Sets

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: