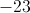Let x be the smallest of the four integers. We are told that the integers are consecutive odd integers. Because odd integers are separated by two, each consecutive odd integer is two larger than the one before it. Thus, we can let x + 2 represent the second integer, x + 4 represent the third, and x + 6 represent the fourth. The sum of the four integers equals 96, so we can write the following equation:

x + (x + 2) + (x + 4) + (x + 6) = 96

Combine x terms.

4x + 2 + 4 + 6 = 96

Combine constants on the left side.

4x + 12 = 96

Subtract 12 from both sides.

4x = 84

Divide both sides by 4.

x = 21

This means the smallest integer is 21. The other integers are therefore 23, 25, and 27.

The question asks us how many of the four integers are prime. A prime number is divisible only by itself and one. Among the four integers, only 23 is prime. The number 21 is divisible by 3 and 7; the number 25 is divisible by 5; and 27 is divisible by 3 and 9. Thus, 23 is the only number from the integers that is prime. There is only one prime integer.

The answer is 1. 

Assume the three consecutive integers equal , , and . The sum of these three integers is 60. Thus,

There are 5 numbers in the sequnce.

How many numbers are left over if you divide 5 into 457?

There would be 2 numbers!

The second number in the sequence is 9,5,6,2,1

Since  are consecutive integers, we know that at least 2 of them will be even. Since we have 2 that are going to be even, we know that when we divide the product by 2 we will still have an even number.  Since 2 is the only prime that is even, we must have:

What we notice, however, is that for , we have the product is 0.  For , we have the product is 24.  We will then never have a product of 4, meaning that is never going to be a prime number.

Consecutive odd integers can be represented as x, x+2, x+4, and x+6.

We know that the sum of these integers is 32. We can add the terms together and set it equal to 32:

x + (x+2) + (x+4) + (x+6) = 32

4x + 12 = 32

4x = 20

x = 5; x+2=7; x+4 = 9; x+6 = 11

Our integers are 5, 7, 9, and 11.

The difference between each number in the series is 9. You can substract nine 11 times from 100 to get 1: 100 – 9x11 = 1. Counting 100, there are 12 positive numbers in the series.

Let's call the first term in the sequence a₁ and the nth term a_n. 

We are told that each term is r times larger than the one before it. Thus, we can find the next term in the sequence by multiplying by r. 

a₁ = a₁

a₂ = r(a₁)

a₃ = r(a₂) = r(r(a₁)) = r²(a₁)

a₄ = r(a₃) = r(r²(a₁)) = r³(a₁)

a_n = r^(n–1)a₁

We can use this information to find r.  

The problem gives us the value of the third and the sixth terms. 

a₃ = r²(a₁) = 12

a₆ = r⁵(a₁) = 96

Let's solve for a₁ in terms of r and a₃. 

a₁ = 12/(r²)

Let's then solve for a₁ in terms of r and a₆.

a₁ = 96/(r⁵)

Now, we can set both values equal and solve for r.

12/(r²) = 96/(r⁵)

Multiply both sides by r⁵ to get rid of the fraction.

12r⁵/r² = 96

Apply the property of exponents which states that a^b/a^c = a^b–c.

12r³ = 96

Divide by 12 on both sides.

r³ = 8

Take the cube root of both sides.

r = 2

This means that each term is two times larger than the one before it, or that each term is one half as large as the one after it. 

a₂ must equal a₃ divided by 2, which equals ¹²/₂ = 6.

a₁ must equal a₂ divided by 2, which equals ⁶/₂ = 3.

Here are the first eight terms of the sequence:

3, 6, 12, 24, 48, 96, 192, 384

The question asks us to find the sum of all the terms less than 250. Only the first seven terms are less than 250. Thus the sum is equal to the following:

sum = 3 + 6 + 12 + 24 + 48 + 96 + 192 = 381

The sequence is geometric with a common ratio of .

The formula for finding the  term of the sequence is 

.

So 

. 

Natural numbers are defined as whole numbers 1 and above. II, IV, V are not natural numbers.