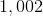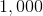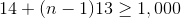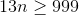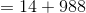All SAT Math Resources
Example Questions
Example Question #31 : Sequences
You are given a sequence with the same difference between consecutive terms. We know it starts at 

From the given information, we know 
Example Question #10 : How To Find The Nth Term Of An Arithmetic Sequence
An arithmetic sequence begins as follows:
Give the sixteenth term of this sequence.
None of the other responses give the correct answer.
Subtract the first term 


Setting 
The 
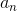
Setting 


Example Question #11 : Nth Term Of An Arithmetic Sequence
An arithmetic sequence begins as follows: 14, 27, 40...
What is the first four-digit integer in the sequence?
Given the first two terms 


Setting 

The 
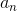
Since we are looking for the first four-digit whole number - equivalently, the first number greater than or equal to 1,000:
Setting 


Therefore, the 77th term, or 




the correct choice.
Example Question #1 : How To Find The Next Term In An Arithmetic Sequence
Each term in the sequence is one less than twice the previous term.
So, 
Example Question #2 : How To Find The Next Term In An Arithmetic Sequence
What is the next number in the following series: 0, 3, 8, 15, 24 . . . ?
32
35
37
40
41
35
The series is defined by n2 – 1 starting at n = 1. The sixth number in the series then equal to 62 – 1 = 35.
Example Question #391 : Arithmetic
A sequence of numbers is as follows:
What is the sum of the first seven numbers in the sequence?
621
248
490
719
1529
621
The pattern of the sequence is (x+1) * 2.
We have the first 5 terms, so we need terms 6 and 7:
(78+1) * 2 = 158
(158+1) * 2 = 318
3 + 8 + 18 +38 + 78 + 158 + 318 = 621
Example Question #2 : How To Find The Next Term In An Arithmetic Sequence
Find the next term of the following sequence:
More information is needed
The sequence provided is arithmetic. An arithmetic sequence has a common difference between each consecutive term. In this case, the difference is 

You can also use a formula to find the next term of an arithmetic sequence:
where 

Example Question #5 : How To Find The Next Term In An Arithmetic Sequence
Solve each problem and decide which is the best of the choices given.
Find the sixth term in the following arithmetic sequence.
First find the common difference of the sequence,
Thus there is a common difference of

so follow that pattern for another 

Example Question #6 : How To Find The Next Term In An Arithmetic Sequence
Find the missing number in the sequence:
The pattern of this sequence is 



For the fourth term, 

Example Question #7 : How To Find The Next Term In An Arithmetic Sequence
An arithmetic sequence begins as follows:
Express the next term of the sequence in simplest radical form.
Using the Product of Radicals principle, we can simplify the first two terms of the sequence as follows:
The common difference 
Add this to the second term to obtain the desired third term:

All SAT Math Resources